（1）不等式的性质
一．选择题（本大题共10小题，每小题5分，共50分）
1．如果a<b<0，则下列不等式中成立的只有 （ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
２．对于任意实数a、b、c、d，命题①
；②
③
；④
；⑤
．其中真命题的个数是 （ ）
Ａ．１ Ｂ．２ Ｃ．３ Ｄ．４
3．不等式“a+b>
Ａ．
Ｂ．
Ｃ．
Ｄ．
4． 若a、b 为实数，则a >b>0是a 2>b2的 （ ）
Ａ．充分不必要条件 Ｂ．必要不充分条件
Ｃ．充要条件 Ｄ．既非充分条件也非必要条件
5．若扇形的周长为C，则使扇形的面积最大时的半径是 （ ）
A．
B．
C．
D．
6．下列函数中，最小值为2
的是 （ ）
A．
B．
C．
D．
7．设
，则下列不等式成立的是 （ ）
A．
B．
C．
D．
8．若
则下列不等式中正确的是 （ ）
A．
B．
C．
D．
9．若实数a、b满足
（ ）
A．8 B．4
C．
D．
10．甲、乙两工厂2002年元月份产值相同，甲厂的产值逐月增加，且每月增加的产值相等，乙厂的产值也逐月增加，且每月增长的百分率相等，已知2003年元月份两厂的产值相等，则2002年7月份产值高的工厂是 （ ）
A．甲厂 B．乙厂 C．产值一样 D．无法确定
二．填空题（本大题共4小题，每小题6分，共24分）
11．若
，
，则a－b的取值范围是
．
12．函数
的值域为 ．
13．已知x>0，y>0且x+y=5，则lgx+lgy的最大值是 ．
14．已知
之间的大小关系是
三．解答题（本大题共6题，共76分）
15．设
，求
的取值范围．（12分）
16．已知x>0，y>0且x+2y=1，求xy的最大值，及xy取最大值时的x、y的值． （12分）
17．已知
与
的大小，并加以证明．（12分）
18．已知△ABC内接于单位圆，且
，
（1）求证内角C为定值；（2）求△ABC面积的最大值． （12分）
19．一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往
km，问这批物资全部到达灾区，最少要多少小时？
（14分）
20．已知a，b，c是实数，
．
（1）求证：
，（2）求证：当
．（14分）
参考答案
一．选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | C | A | C | C | B | C | B | A |
二．填空题（本大题共4小题，每小题6分，共24分）
11． 
12． 
13．
14．
15．（12分）
[解析]：因为
，
，
+
又
所以
16．（12分）
[解析]：因为x >0，y>0，且x +2y=1
所以x y= 
=
当且仅当x =2y时上述不等式取“=”号，由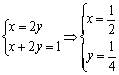
因此，当
，
时，x y取得最大值
．
17．（12分）
[解析]：
，
因为
，所以
（当且仅当
时取“=”号）．
①当a>1时，
，
，
即
（当且仅当时取“=”号）．
②当0<a<1时，
，
即
（当且仅当
时取“=”号）．
18．（12分）
（1）[证明]：由
即
，所以∠
（2）[解析]：由题意可得
当AC=BC时，
有最大值，最大值为
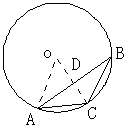
再作辅助线如图，连结OD，OA，得AB⊥OC，
所以AD=BD= 
，CD=1－，
AC2=AD2+CD2= 
所以最大值=
= 
19．（14分）
[解析]：设全部物资到达灾区所需时间为t小时，由题意可知，
t相当于：最后一辆车行驶了25个km+400（km）所用的时间，
因此，t=
当且仅当
即x =80时取“=”号．
答：这些汽车以
20．（14分）
[证明]（1）
（2）
即
的图象是一条直线．
上的最大值只能在
处取得
．