高二文科数学第二学期期中考试 数学(文科)
一、选择题（本大题共10小题，每题5分，共50分）
1．已知命题 
R，
，则 （ ）
A．
R, 
B．
R,
C．R, 
D．R,
2．“p
q为真”是“
p为假”的
（ ）
A．充分不必要条件. B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
3．“
”成立的一个充分而不必要条件是 （ ）
A．
．
B．
．
C．或
．
D．或
．
4．曲线
在点
处的切线与坐标轴所围三角形的面积为 （ ）
A．
B．
C．
D．
5．椭圆的焦距为2,则m的值等于 （ ）
A．5或3 B．
6．设甲、乙、丙、丁是四个命题，甲是乙的充分而不必要条件，丙是乙的充要条件，丁是丙的必要而不充分条件，那么丁是甲的 （ ）
A．充分不必要条件. B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
7．已知P是双曲线
上一点，双曲线的一条渐近线方程为3x-2y=0,F1 、F2分别是双曲线的左、右焦点，若P F1 =3，则P F2=
（ ）
A．7 B．
8．△ABC一边的两个顶点为B（
3，0），C（3，0）另两边所在直线的斜率之积为
（ 为常数），则顶点A的轨迹不可能落在下列哪一种曲线上 （ ）
A．圆 B．椭圆 C．双曲线 D．抛物线
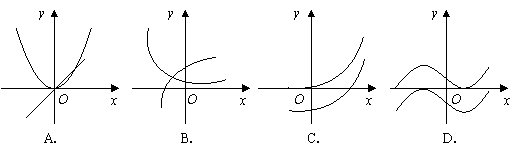
9．设
是函数
的导函数，将
和
的图象画在同一个直角坐标系中，不可能正确的是 （ ）
 |
| |
，直线
，当
时，直线
恒在曲线C的上方，则实数
的取值范围是 （ ）
A．
B．
C．
D．
二、填空题（本大题有5小题，每小题4分，共20分）
11．抛物线
的焦点到准线的距离为______________.
12．命题“若a=1, 则a2=
13．设
为双曲线
的两个焦点，点
在双曲线上且满足
，则
的面积是____________________
14．若椭圆
的左、右焦点分别为，线段
被抛物线
的焦点
分成5﹕3的两段，则此椭圆的离心率为 .
15．若函数
在区间（
）上既不是单调递增函数，也不是单调递减函数，实数a的取值范围是______________________.
三、解答题（本大题共6小题，16——19每题13分，20、21每题14分，共80分）
16．已知函数
（1）求的单调减区间；
（2）若在区间[－2，2]上的最大值为20，求a的值.
17．抛物线C的顶点在原点，焦点F与双曲线
的右焦点重合，过点P（2，0）且斜率为1的直线l与抛物线C交于A、B两点。
（1）求弦长AB；
（2）求弦AB中点到抛物线准线的距离。
18．已知函数f（x）＝x3＋ax2＋bx＋c在x＝－
与x＝1时都取得极值.
（1）求a、b的值；
（2）若函数f（x）的图象与x轴有3个交点，求c的取值范围。
19．已知双曲线
及点A（
，0）。
（1）求点A到双曲线一条渐近线的距离；
（2）已知点O为原点，点P在双曲线上，△POA为直角三角形，求点P的坐标。
20．椭圆C的中心为坐标原点O，焦点在x轴上，离心率
，且椭圆过点（2，0）。
（1）求椭圆方程；
（2）求圆
上的点到椭圆C上点的距离的最大值与最小值。
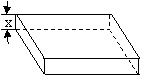
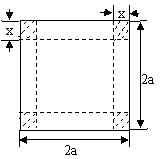
21．从边长
（1）把铁盒的容积V表示为x的函数，并指出其定义域；
（2）x为何值时，容积V有最大值.
参考答案
一、选择题
| |
二、填空题
11．
12. 若a2=1, 则a=1 13.1 14.
15.(
)
三、解答题
16．（1）（-∞，-1），（3，+∞）；（2）A=-2.
17．（1）AB=
; (2) 11.
18．（1）
,
(2)
.
19．（1） 
； （2）
或
。
20．（1）
； （2）最大值为
最小值为.
21．（1）
定义域为
。
（2）
。