高二文科数学第二学期期中考试2

高二数学试题（文科）

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 共150分，考试时间120分钟.

注意事项：

1、所有题目用钢笔或圆珠笔直接答在答题卷中，只能在各题目答题区域内作答，超出黑色矩形边框限定区域的答案无效。

2、答卷前将答题卷上的姓名、考号、班级填写清楚。

第Ⅰ卷（选择题 共60分）

一、选择题：本大题共12题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.

1、且，则…等于（　 ）

A、　　　　　　　　　　 B、　　　　　　　　　　C、　　　　　　　　　 D、

2、已知直线，直线，给出下列命题：

①∥  ②∥ ③∥ ④∥

其中真命题的是（　 ）A、①②③　　B、②③④　 C、②④　　 D、①③

3、一个正四棱锥的底面面积为Q，则它的中截面(过各侧棱的中点的截面)的边长是（　 ）　　A、　　 　 B、　　　C、　　　D、

4、α表示一个平面，表示一条直线，则α内至少有一条直线与直线（　 ）

A、平行　　　　　B、相交　　　　  C、异面　　　　 D、垂直

5、设M=，N=，P=，Q=，则四个集合的关系为（　 ）

A、　　　　　  B、

C、　　　　　  D、

6、设正方体的全面积为，一个球内切于该正方体，那么这个球的体积是（　）

A、　　　　　　　　 B、 　 C、　　 D、

7、某电视台连续播放5个广告，其中3个不同的商业广告和2个不同的奥运广告，要求最后播放的必须是奥运广告，且2个奥运广告不能连续播放，则不同的播放方式有（　 ）A、36种　　　　 B、48种　　　　  C、 120种　 　　D、20种

8、已知北纬45⁰圈上有A、B两地，且A地在东经30⁰线上，B地在西经60⁰线上，设地球半径为R，则A、B两地的球面距离是（　 ）

A、　　　　　  B、　　　　C、　　　　  D、

9、若直线与平面所成角为，直线a在平面内，且与直线异面，则直线与直线a所成的角的取值范围是（　 ）

A、　　　　 B、　　　　C、 　　 D、

10、正四面体棱长为，点在上移动，点在上移动，则的最小值为（　） A、　 B、　　　 C、　　　 D、

11、若集合，集合，是从到的映射，则满足的映射有（　）A、6个 B、7个 C、8个 D、9个

12、正方体中，是，的交点，则与所成的角是（　）A、60° B、90° C、 D、

　第Ⅱ卷（非选择题 共90分）

二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在题中横线上.

13、　　　　　　　 .

14、是球面上的四个点，两两垂直，且，则该球的表面积为_______________.

15、正六棱锥S-ABCD的底面边长为6，侧棱长为，则它的侧面与底面所成的二面角的大小为_________.

16、已知是直线，是平面，给出下列命题：

①、若，，则　　　　　 ②、若与所成角相等，则

③、若，，则　　　　　④、若，，则，

其中真命题的序号是_______________.

三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.

17、（本小题满分12分）

已知ABCD是正方形，PA⊥平面ABCD，且PA=AB=，E、F是

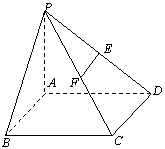侧棱PD、PC的中点。 （1）求证：EF∥平面PAB ；

（2）求直线PC与底面ABCD所成角的正切值。

18、（本小题满分12分）

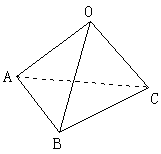已知球面上的三点A、B、C，且AB=6，BC=8，AC=10，球O的半径R=13，求球心O到面ABC的距离。

19、（本小题满分12分）

有4名老师和4名学生站成一排照相。（必须写出解析式再算出结果才能给分）

（1）4名学生必须排在一起，共有多少种不同的排法？

（2）任两名学生都不能相邻，共有多少种不同的排法？

（3）老师和学生相间排列，共有多少种不同的排法？

20、（本小题满分12分）

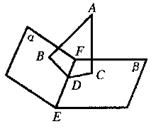
二面角α–EF–β的大小为120°，A是它内部的一点AB⊥α，AC⊥β，B，C分别为垂足.

（1）求证：平面ABC⊥β；

（2）当AB=4cm，AC=6cm,求BC的长及A到EF的距离.

21、（本小题满分12分）

已知正四棱柱ABCD—A₁B₁C₁D₁.AB=1，AA₁=2，点E为CC₁中点，点F为BD₁中点.

（1）证明EF为BD₁与CC₁的公垂线；

（2）求点D₁到面BDE的距离.

22、（本小题满分14分）

已知正三棱柱ABC—A₁B₁C₁的每条棱长均为a，M为棱A₁C₁上的动点．

（1）当M在何处时，BC₁//平面MB₁A，并证明之；

（2）在（1）下，求平面MB₁A与平面ABC所成的二面角的大小；

（3）求B—AB₁M体积的最大值．

重庆市暨华中学2007-2008学年度第二学期期中考试

高二数学答题卷（文科）

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

　　 13.　　　　　 　　14.　　　　　　　　 　 15.　　　　　　 16.　　　　　　 

17.（本小题满分12分）

三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤

18.（本小题满分12分）

19.（本小题满分12分）

重庆市暨华中学2007-2008学年度第二学期期中考试

高二数学参考答案（文科）

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	C	D	A	D	A	D	A	B	C	B	B	D

二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上.

13.　　5　　　 14.　　　　　　15. 　　　　16.①④

三、解答题：本大题共6小题，共76分.解答应写出文字说明，证明过程或演算步骤.

17.（本小题满分12分）

解：证明：（1）

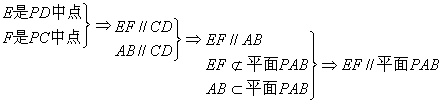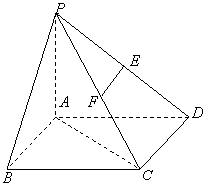
证明：（2）连结AC，因为PA平面ABCD，所以就为直线PC与平面ABCD所成的角。即

又因为正方形ABCD的边长为，所以AC=，

所以

18.（本小题满分12分）

解：,是直角三角形。

因为球心O在面ABC的射影M是所在截面圆的圆心，

即的外心。

所以M是直角三角形ABC斜边AC的中点，且.

在中，.

所以球心到面ABC的距离为12.

19.（本小题满分12分）

（I）用“捆绑法”得=2880；　　（4分）

（II）用“插空法”得=2880；　　　 （8分）

（III）只有两种间隔法，可得2=1152　（12分）

20.（本小题满分13分）

（1）∵AB⊥α，EFα，∴EF⊥AB，同理EF⊥AC，AB，AC是两条相交直线，∴ EF⊥平面ABC，∵ EFα，EFβ,∴ 平面ABC⊥平面α,平面ABC⊥平面β。

  （2）设平面ABC与EF交于点D，连结BD，CD，则BD，CD平面ABC，∵EF⊥平面ABC，∴ EF⊥BC，EF⊥DC，∠BDC是二面角α–EF–β的平面角，∠BCD=120°，A，B，C，D在同一平面内，且∠ABD=∠ACD=90°，

∴∠BAC=60°，当AB=4 cm, AC=6 cm时，

BC=

又∵  A，B，C，D共圆，∵AD是直径。∵ EF⊥平面ABC，AD平面ABC，

∴ AD⊥EF，即AD是A到EF的距离，由正弦定理，得AD==（cm）

21. （本小题满分12分）

（1）证法一：取BD中点M.连结MC，FM .

　 ∵F为BD₁中点 ，　　∴FM∥D₁D且FM=D₁D .（2分）

　 又EC=CC₁且EC⊥MC ，∴四边形EFMC是矩形　　　　

　 ∴EF⊥CC₁.（4分） 又CM⊥面DBD₁ .∴EF⊥面DBD₁ .　　

　 ∵BD₁面DBD₁ . ∴EF⊥BD₁ .　故EF为BD₁ 与CC₁的公垂线.

（Ⅱ）解：连结ED₁，有V_E－DBD1=V_D1－DBE .

由（Ⅰ）知EF⊥面DBD₁ ，设点D₁到面BDE的距离为d.

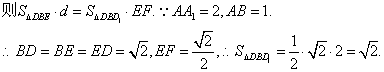
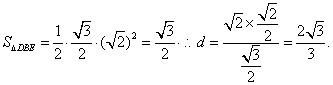
故点D₁到平面DBE的距离为.

法2：建立空间直角坐标系D-xyz如图所示。易得面DBE的一个法向量。

　 所以D₁到平面DBE的距离.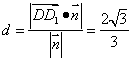　　

22. （本小题满分14分）

解：（I）当M在A₁C₁中点时，BC₁//平面MB₁A

∵M为A₁C₁中点，延长AM、CC₁，使AM与CC₁延长线交于N，则NC₁=C₁C=a

连结NB₁并延长与CB延长线交于G，则BG=CB，NB₁=B₁G　　 （2分）

在△CGN中，BC₁为中位BC₁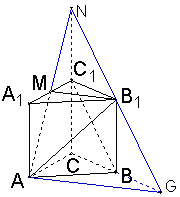//GN

又GN平面MAB₁，∴BC₁//平面MAB₁ （4分）

（II）∵△AGC中， BC=BA=BG　　 ∴∠GAC=90°

 即AC⊥AG　　 又AG⊥AA₁　　

 　　 （6分）

 ∴∠MAC为平面MB₁A与平面ABC所成二面角的平面角

 

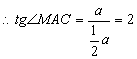
 ∴所求二面角为　　　　　　　 （8分）

（Ⅲ）设动点M到平面A₁ABB₁的距离为h_M．

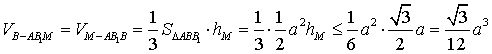
　即B—AB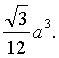₁M体积最大值为此时M点与C₁重合．　 （14分）