高二文科数学第二学期期中考试试卷()
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求
1.已知![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2.在复平面内,复数![]() +(1+
+(1+![]()
![]() )2对应的点位于( )
)2对应的点位于( )
A. 第一象限 B. 第二象限 C.第三象限 D.第四象限
3.下列函数中哪个与函数y=x是同一个函数 ( )
A.![]() B. y=
B. y=![]() C.
C. ![]() D. y=
D. y=![]()
4. 已知x与y之间的一组数据:
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
则y与x的线性回归方程为y=bx+a必过( )
A.点![]() B.点
B.点![]() C.点
C.点![]() D.点
D.点![]()
5.函数f (x)的定义域是[0,2],函数g (x) = f (x +![]() ) – f (x –
) – f (x –![]() )的定义域是
)的定义域是
A.[0,2] B.[–![]() ,
,![]() ] C.[
] C.[![]() ,
,![]() ]
D.[
]
D.[![]() ,
,![]() ]
]
6. 、实数a、b、c不全为0的条件是( )。
A.a、b、c均不为0; B.a、b、c中至少有一个为0;
C.a、b、c至多有一个为0; D.a、b、c至少有一个不为0。
7.已知函数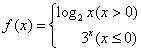 ,则
,则![]() 的值为( )
的值为( )
A. 9
B.![]() C.
C.![]() D.
D.![]()
8、类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列哪些性质,你认为比较恰当的是( )。
①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等。
A.①; B.①②; C.①②③; D.③。
9. 下面几种推理是合情推理的是( )
(1)由圆的性质类比出球的有关性质;
(2)由直角三角形、等腰三角形、等边三角形内角和是![]() ,归纳出所有三角形的内角和都是
,归纳出所有三角形的内角和都是![]() ;
;
(3)某次考试张军成绩是100分,由此推出全班同学成绩都是100分;
(4)三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]()
A.(1)(2) B.(1)(3) C.(1)(2)(4) D.(2)(4)
10. 设![]() ,用二分法求方程
,用二分法求方程![]() 内近似解的过程中取区间中点
内近似解的过程中取区间中点![]() ,那么下一个有根区间为 ( )
,那么下一个有根区间为 ( )
A.(1,2) B.(2,3) C.(1,2)或(2,3)都可以 D.不能确定
11.已知函数![]() 是
是![]() 偶函数,它在
偶函数,它在![]() 上是增函数,若
上是增函数,若![]() ,则
,则![]() 的取值范围( )
的取值范围( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.设函数![]() 是
是![]() 上的增函数,且
上的增函数,且![]() ,则方程
,则方程![]() 在
在
![]() 内( )
内( )
A.可能有三个实根 B.可能有2个实数根
C.有唯一的实数根 D.没有实数根
乐桥中学2007-2008学年度第二学期期中考试
一、选择题 高二数学答题卷
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷(非选择题 共90分)
| 得分 | 评卷人 | 二.填空题:本大题共有4小题,每小题4分,共16分.把答案填在题中横线上. |
13. 对于一组数据的两个函数模型,其残差平方和分别为153.4 和200,若从中选取一个拟合程度较好的函数模型,应选残差平方和为_______的那个
14..从![]() 中,可得到一般规律为 (用数学表达式表示)
中,可得到一般规律为 (用数学表达式表示)
15. 设![]() ,则函数
,则函数![]() 的最大值是___________最小值是_________
的最大值是___________最小值是_________
16. 有以下命题:
(1)若函数f(x),g(x)在R上是增函数,则f(x)+g(x)在R上也是增函数;
(2)若f(x)在R上是增函数,g(x)在R上是减函数,则g(x)-f(x)在R上是减函数;
(3)若函数f(x)在区间[a,b]上递增,在(b,c)上也递增,则f(x)在![]() 上递增;
上递增;
(4)若奇函数f(x)在![]() 上递减,则f(x)在
上递减,则f(x)在![]() 上也递减。
上也递减。
其中正确命题的的序号为 ____________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
| 得分 | 评卷人 | 17.(本小题满分12分) |
已知复数z1满足(1+i)z1=-1+5i, z2=a-2-i,
其中i为虚数单位,a∈R, 若![]() <z1,求a的取值范围.
<z1,求a的取值范围.
| 得分 | 评卷人 | 18.(本小题满分12分) |
已知集合![]() ,集合
,集合![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
| 得分 | 评卷人 | 19.(本小题满分12分) |
.在各项为正的数列![]() 中,数列的前n项和
中,数列的前n项和![]() 满足
满足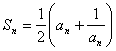
(1) 求![]() ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列![]() 的通项公式;(3) 求
的通项公式;(3) 求![]()
|
|
| 得分 | 评卷人 | 20.(本小题满分12分) |
已知![]() ,
,![]() 是二次函数,
是二次函数,![]() 是奇函数,且当
是奇函数,且当![]() 时,
时,![]() 的最小值是1,求
的最小值是1,求![]() 的表达式.
的表达式.
| 得分 | 评卷人 | 21.(本小题满分12分) |
某租赁公司拥有汽车100辆. 当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆. 租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
| 得分 | 评卷人 | 22.(本小题满分14分) |
集合![]() 是由适合以下性质的函数组成:对于任意
是由适合以下性质的函数组成:对于任意![]() ,
,![]() ,且
,且![]() 在
在![]() 上是增函数,
上是增函数,
1)试判断![]() 及
及![]() 是否在集合
是否在集合![]() 中,若不在
中,若不在![]() 中,试说明理由;
中,试说明理由;
(2)对于(1)中你认为集合![]() 中的函数
中的函数![]() ,不等式
,不等式![]()
![]() 是否对任意
是否对任意![]()
![]() 恒成立,试证明你的结论
恒成立,试证明你的结论
高二文科数学期中试题答案
一选择题1
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | C | D | D | D | B | C | C | A | B | C |
二填空题
13.153.4
14.![]()
15. ![]() ,
,![]() 16.
(1),(2),(4)
16.
(1),(2),(4)
三解答题
17解:由题意得 z1=![]() =2+3i,
=2+3i,
于是![]() =
=![]() =
=![]() ,
,![]() =
=![]() .
.
![]() <
<![]() , 得a2-
, 得a2-
18解:![]() ,若
,若![]() ,则
,则
(1)若![]() 时,
时,![]() 有
有![]()
(2)若![]() 时,有
时,有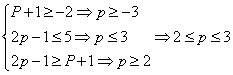
![]() 可得实数
可得实数![]() 的取值范围为
的取值范围为![]()
19(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
20.解:设![]() ,则
,则
![]() 又
又![]() 为奇函数,
为奇函数,
![]() 对
对![]() 恒成立,
恒成立,
![]() ,解得
,解得![]() ,
, ![]() ,其对称轴为
,其对称轴为![]() .
.
(1) 当![]() 即
即![]() 时,
时,![]() ;
;
(2) 当![]() 即
即![]() 时,
时,![]() 解得
解得![]() 或
或![]() (舍) ;
(舍) ;
(3) 当![]() 即
即![]() 时,
时,![]() (舍),
(舍),
综上知![]() 或
或![]()
21. .解:(1)当每辆车的月租金定为3600元时,未租出的车辆数为![]()
所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益为
![]() ,
,
整理得![]() .
.
所以,当x=4050时,![]() 最大,最大值为
最大,最大值为![]() ,
,
答:当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大月收益为307050元.
22. 解:(1)当![]() 时,
时,![]()
![]() ,所以
,所以![]() ,又
,又![]() 值域为
值域为![]() ,所以
,所以![]() ; 当
; 当![]() 时
时![]() 为增函数,所以
为增函数,所以![]() .
.
(2)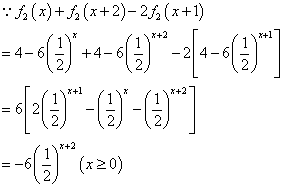
![]() 对任意
对任意![]() 不等式
不等式![]() 总成立,
总成立,