高二理科下学期期中考试数学试题
(考试时间:120分钟 总分:150分)
命题人:周湖平
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列命题不正确的是 ( D )
A 使用抽签法,每个个体被抽中的机会相等;
B 使用系统抽样从容量为N的总体中抽取容量为n的样本,确定分段间隔k时,若![]() 不是整数,则需随机地从总体中剔除几个个体;
不是整数,则需随机地从总体中剔除几个个体;
C 无论采取怎样的抽样方法,必须尽可能保证样本的代表性.
D分层抽样就是随意的将总体分成几部分
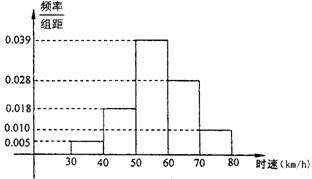
2. 200辆汽车正经过某一雷达地区,这些汽车运行的时速频率分布直方图如图所示,则时速超过
|
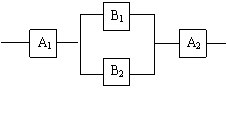 3.一个元件能正常工作的概率叫做这个元件的可靠性,设构成系统的每个元件的可靠性均为
3.一个元件能正常工作的概率叫做这个元件的可靠性,设构成系统的每个元件的可靠性均为![]() ,且各个元件能否正常工作是相互独立的,则如图由4个元件构成系统的可靠性为 ( D
)
,且各个元件能否正常工作是相互独立的,则如图由4个元件构成系统的可靠性为 ( D
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 已知随机变量ξ~ B(n,p)且Eξ= 2.4,Dξ= 1.44,,则参数n,p的值为( )
A.n =
4, p = 0.6 B.n = 6, p = 0.
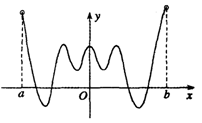 5 、函数y=f (x)定义域为(a,b),y=f ' (x)在(a,b)上的图象如图,则y=f (x)在区间(a,b)上极大值点的个数为 ( B )
5 、函数y=f (x)定义域为(a,b),y=f ' (x)在(a,b)上的图象如图,则y=f (x)在区间(a,b)上极大值点的个数为 ( B )
A.1 B.2
C.3 D.4
 6.
如图所示的是2008年北京奥运会的会徽,其中的“中国印”的外边是由四个色块构成,可以用线段在不穿越另两个色块的条件下将其中任意两个色块连接起来(如同架桥),如果用三条线段将这四个色块连接起来,不同的连接方法共有
( C )
6.
如图所示的是2008年北京奥运会的会徽,其中的“中国印”的外边是由四个色块构成,可以用线段在不穿越另两个色块的条件下将其中任意两个色块连接起来(如同架桥),如果用三条线段将这四个色块连接起来,不同的连接方法共有
( C )
A. 8种 B. 12种 C. 16种 D. 20种
7.2007年12月中旬,我国南方一些地区遭遇历史罕见的雪灾,电煤库存吃紧.为了支援南方地区抗灾救灾,国家统一部署,加紧从北方采煤区调运电煤. 某铁路货运站对6列电煤货运列车进行编组调度,决定将这6列列车编成两组,每组3列,且甲、乙两列列车不在同一小组.如果甲所在小组3列列车先开出,那么这6列列车先后不同的发车顺序共有 ( C )
(A)36种 (B)108种 (C)216种 (D)432种
8.已知函数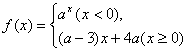 满足对任意
满足对任意![]() 成立,则a的取值范围是 ( A )
成立,则a的取值范围是 ( A )
A.![]() B.(0,1) C.
B.(0,1) C.![]() D.(0,3)
D.(0,3)
9.设函数![]() 的最大值为3,则f(x)的图象的一条对称轴的方程是
( A
)
的最大值为3,则f(x)的图象的一条对称轴的方程是
( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 某市统考成绩大体上反映了全市学生的成绩状况,因此可以把统考成绩作为总体,设平均成绩![]() ,标准差
,标准差![]() ,总体服从正态分布,若全市重点校录取率为40%,那么重点录取分数线可能划在(已知φ(0.25)=0.6)
( C )
,总体服从正态分布,若全市重点校录取率为40%,那么重点录取分数线可能划在(已知φ(0.25)=0.6)
( C )
A.525分 B.515分 C.505分 D.495分
11.若m、n、l是互不重合的直线,![]() 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题:
①若![]()
| |
③若m不垂直于![]() 内的无数条直线
内的无数条直线
④若![]()
⑤若![]()
其中正确命题的序号是 ( D )
A.①③ B.②④ C.②③④ D.②④⑤
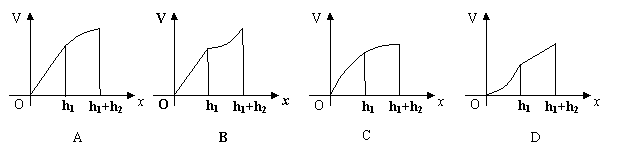
12.如图,是一个由圆锥与圆柱叠成的组合体,一个平面自圆柱的上底面出发向下平移至圆锥的顶
 点为止,若平面截组合体的上部分体积为V,平面与上底面的距离为
点为止,若平面截组合体的上部分体积为V,平面与上底面的距离为![]() ,则函数
,则函数![]() 的图象大致是( A )
的图象大致是( A )
 |
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
13、二项式![]() 展开式中的常数项为 7 .
展开式中的常数项为 7 .
14、已知![]() ,记
,记![]() ,
,![]() ,
, ![]() =________0_______
=________0_______
15、![]() __2_.
__2_.
16、民间酒座上划酒令:“杠子打老虎,老虎吃鸡,鸡吃虫,虫蛀杠子”,将这四种不同属性的物质任意排成一列,为了避免相克物质相邻,特在这4种物质中插入一种与这4种物质均不相克的物质W,设事件A表示“这5种物质排列中属性相克的两种物质不相邻”,则事件A出现的概率是______![]() __________。
__________。
三.解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
某车间在三天内,每天生产10件某产品,其中第一天,第二天分别生产出了1件、2件次品,而质检部每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(Ⅰ)求第一天通过检查的概率;
(Ⅱ)求前两天全部通过检查的概率;
(Ⅲ)若厂内对车间生产的产品采用记分制:两天全不通过检查得0分,通过1天、2天分别得1分、2分,求该车间在这两天内得分![]() 的数学期望.
的数学期望.
解:(I)![]() 随意抽取4件产品检查是随机事件,而第一天有9件正品
随意抽取4件产品检查是随机事件,而第一天有9件正品
![]() 第一天通过检查的概率为
第一天通过检查的概率为![]() ……3分
……3分
(II)同(I),第二天通过检查的概率为![]()
因第一天,第二天是否通过检查相互独立
所以,两天全部通过检查的概率为:![]() ……6分
……6分
(Ⅲ)记得分为![]() ,则
,则![]() 的值分别为0,1,2
的值分别为0,1,2
![]()
![]()
![]()
因此,![]() ……12分
……12分
18.(本小题满分12分)省教研室准备举行一次高中数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
| 版本 | 人教A版 | 人教B版 | 苏教版 | 北师大版 |
| 人数 | 20 | 15 | 5 | 10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为![]() ,求随机变量
,求随机变量![]() 的变分布列和数学期望。
的变分布列和数学期望。
解:(1)从50名教师随机选出2名的方法数为![]()
选出2人使用版本相同的方法数为![]()
故2人使用版本相同的概率为:
![]() ………5分
………5分
(2)∵![]() ,
, ![]()
![]()
|
| 0 | 1 | 2 |
| P |
|
|
|
∴![]() 的分布列为
的分布列为
…………10分
∴![]() …………12分
…………12分
(![]() 可以不扣分)
可以不扣分)
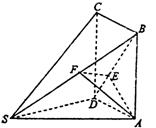
19.(本小题满分12分)如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,
SD⊥AB,且AB=2AD,SD=![]() AD,
AD,
(Ⅰ)求证:平面SDB⊥平面ABCD;
(Ⅱ)求二面角A—SB—D的大小.
解:(1)∵SD⊥AD,SD⊥AB,AD∩AB=A
∴SD⊥平面ABCD,
又∵SD![]() 平面SBD, ∴平面SDB⊥平面ABCD。 …………5分
平面SBD, ∴平面SDB⊥平面ABCD。 …………5分
(2)[解法一]:由(1)知平面SDB⊥平面ABCD,
BD为平面SDB与平面ABCD的交线,过点A作AE⊥DB于E,则AE⊥平面SDB,
又过点A作AF⊥SB于F,连结EF。
由三垂线定理的逆定理得 EF⊥SB,
∴∠AFE为二面角A—SB—D的平面角。 …………8分
在矩形ABCD中,设AD=a,
则![]() ,
,
|
而在Rt△SAD中,SA=
∴SB2=SA2+AB2, …………10分
即△SAB为等腰直角三角形,且∠SAB为直角,
∴![]()
∴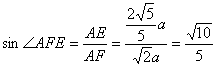
故二面角A—SB—D的大小为
![]() …………12分
…………12分
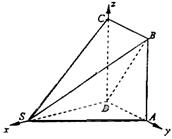
[解法二]:由题可知DS、DA、DC两两互相垂直。
|
设AD=a,
则S(![]()
![]()
∵![]() --------------------7分
--------------------7分
设面SBD的一个法向量为n=(x,y,-1)
则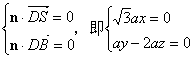
解得 n=(0,2,-1)--------------------9分
又∵
![]()
设面SAB的一个法向量为m=(1,y,z),
则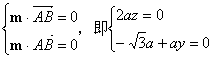
解出
m=(1,![]() ,0), --------------------11分
,0), --------------------11分
![]()
故所求的二面角为arccos![]() --------------------12分
--------------------12分
|
20.(本小题满分12分)
已知函数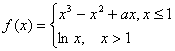 ,在x=1处连续.
,在x=1处连续.
(I)求a的值;
(II)求函数![]() 的单调减区间;
的单调减区间;
(III)若不等式![]() 恒成立,求c的取值范围.
恒成立,求c的取值范围.
(I)解:由![]() 处连续,
处连续,
可得![]() ,故
,故![]() …………3分
…………3分
(II)解:由(I)得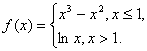
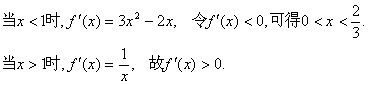
所以函数![]() …………7分
…………7分
(III)解:设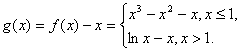

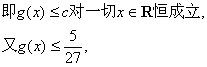
故c的取值范围为![]() …………12分
…………12分
21、(本小题满分12分)已知函数![]() ,在
,在![]() 处取得极值为2。
处取得极值为2。
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)若函数![]() 在区间(m,
在区间(m,
(Ⅲ)若P(x0,y0)为![]() 图象上的任意一点,直线l与
图象上的任意一点,直线l与![]() 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围.
解:(Ⅰ)已知函数![]() ,
,
![]() …………1分
…………1分
又函数![]() 在
在![]() 处取得极值2,
处取得极值2,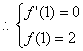 …………2分
…………2分
即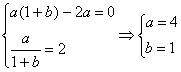
![]() ……………………4分
……………………4分
(Ⅱ)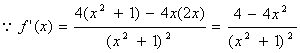 由
由![]() ,得
,得![]() ,
,
即![]()
所以![]() 的单调增区间为(-1,1) …………6分
的单调增区间为(-1,1) …………6分
因函数![]() 在(m,2m+1)上单调递增,
在(m,2m+1)上单调递增,
则有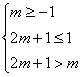 , …………7分
, …………7分
解得![]() 即
即![]() 时,函数
时,函数![]() 在(m,2m+1)上为增函数 …………8分
在(m,2m+1)上为增函数 …………8分
(Ⅲ)![]()
直线l的斜率![]() …………9分
…………9分
即![]()
![]() 令
令![]() , …………10分
, …………10分
则![]()
![]() 即直线l的斜率k的取值范围是
即直线l的斜率k的取值范围是![]() …………12分
…………12分
22.
|
(Ⅰ)试求数列{![]() }的通项公式
}的通项公式![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(Ⅱ)求证:![]()
(Ⅲ)求证:![]() (注:
(注:![]() ).
).
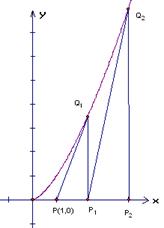
解: (Ⅰ) ![]()
![]() ,若切点是
,若切点是![]() ,则
,则
切线方程为![]() .
1分
.
1分
当n=1时,切线过点(1,0),即![]() ,得
,得![]()
当n>1时,切线过点![]() ,即
,即![]() ,解得
,解得![]() .
.
![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
故所求通项![]() .
4分
.
4分
(Ⅱ) 由(1)知![]()
![]()
![]()
![]() 9分
9分
(Ⅲ)设![]() ,则
,则![]() ,
,
两式相减得![]() ,
,
![]()
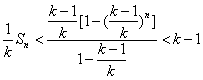 . 故
. 故![]() .
14分
.
14分