高二理科数学下册期中调研测试
数 学 试 卷（理科）
（考试时间120分钟，满分160分）
参考数据
| P（ | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一、填空题：本大题共14题，每小题5分，共70分，请将正确答案填写在答题纸的相应位置．
1．复数z=m(m－1)＋(m－1)i是纯虚数，则实数m的值是 ▲ ．
2．计算
= ▲ ．
3．若由一个2×2列联表中的数据计算得
2=6.825,那么确认两个变量有关系的把握性有 ▲ ．
4．设
，
则
的值为 ▲ ．
5．对于变量x，y随机取到的一组样本数据，用r表示样本相关系数，给出下列说法
①若r＞r0.05，表明有95﹪的把握认为x与y之间具有线性相关关系；
②若r＜r0.05，表明x与y之间一定不具有线性相关关系；
③r的取值范围是[0，1]，且越接近1，线性相关程度越强．
其中正确说法种数是 ▲ ．
6．
圆x2＋y2=1在矩阵A对应的伸压变换下变为椭圆
，则矩阵A是 ▲ ．
7．已知方程
是根据女大学生的身高预报她的体重的回归方程，其中x的单位是cm，
的单位是kg，那么针对某个体（160，53）的随机误差是 ▲ ．
8．抛掷一颗质地均匀的正方体骰子，将向上一面的点数看作随机变量X，则X的方差是 ▲ ．
9．若z是复数，z ＋2－2i=2,则z＋1－i＋z的最大值是 ▲ ．
10．若数列{an}满足a1=3，a2=4，且
（n≥3），则a2007的值为 ▲ ．
11．用0、1、2、3、4这五个数字组成无重复数字的五位数，其中恰有一个偶数数字夹在两个奇数数字之间的五位数的个数是 ▲ ．
12．安排3名支教老师去6所学校任教，每校至多2人，则不同的分配方案共有 ▲ 种.（用数字作答）
13．利用数学归纳法证明不等式
（n>1，nÎN*）的过程中，用n = k+1时左边的代数式减去n = k时左边的代数式的结果为 ▲ ．
14． 如图（1）直线l∥AB，且与CA，CB分别相交于点E，F，EF与AB间的距离是d，点P是线段EF上任意一点，Q是线段AB上任意一点，则PQ的最小值等于d．
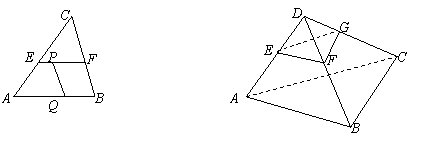
类比上述结论我们可以得到：在图（2）中，平面α∥平面ABC，且与DA，DB，DC分别相交于点E，F，G，平面α与平面ABC间的距离是m， ▲ ．
二、解答题：本大题共6小题；共90分．解答应写出文字说明、证明过程或演算步骤．
15．（本小题满分14分）某厂生产的A产品按每盒10件进行包装，每盒产品均需检验合格后方可出厂.质检办法规定：从每盒10件A产品中任抽4件进行检验，若次品数不超过1件，就认为该盒产品合格；否则，就认为该盒产品不合格.已知某盒A产品中有2件次品.求：(1)该盒产品被检验合格的概率；
(2)若对该盒产品分别进行两次检验，则两次检验得出的结果不一致的概率.
16．（本小题满分14分）二阶矩阵M对应的变换将点(1,－1)与(－2,1)分别变换成点
(－1,－1)与(0，－2).
(Ⅰ) 求矩阵M；
(Ⅱ) 设直线l在变换M作用下得到了直线m：x－y=4，求l的方程．
17．（本小题满分14分）已知
的展开式的各项系数之和等于
展开式中的常数项，求展开式中含
的项的二项式系数．
18、（本小题满分16分）某城市有甲、乙、丙、丁4个旅游景点，一位客人游览这4个景点的概率都是0.6，且客人是否游览哪个景点互不影响．设
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值．
（Ⅰ）求的分布列及数学期望；
(Ⅱ) 记“函数
在区间
上单调递增”为事件A，求事件A的概率．
19．（本小题满分16分）设复数 z 满足：（2－＋i）z在复平面上对应的点在第二、四象限的角平分线上，且z－1是z和z－2的等比中项，求z．
20．(本题16分)设
(n∈N*)，是否存在整式
，使得
a1+a2+…+ an－1=
对n≥2的一切自然数都成立，并证明你的结论.