高二理科数学下期期中考试
数学试卷(理科)2008-4
本试卷分填空题和解答题两部分。满分160分,考试时间120分钟。
一、填空题(本大题共14小题,每题5分,共70分)
1、在用反证法证明“圆内不是直径的两弦,不能互相平分”,假设 。
2、在三角形中,有结论:“三角形ABC中,AB+BC>AC”。类似地,在四面体P-ABC中有
。
3、如果今天是星期一,从明天开始,![]() 天后地第一天是星期
。
天后地第一天是星期
。
4、![]() 。(结果用式子表示)
。(结果用式子表示)
5、4男3女站成一排照相,要求男女各不相邻,则共有 种不同的站法。
6、从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有 。
7、若 ![]() ,
, ![]() ,且
,且![]() 为纯虚数,则实数
为纯虚数,则实数![]() 的值为
。
的值为
。
8、如果![]() 的展开式中系数绝对值最大的项是第4项,则
的展开式中系数绝对值最大的项是第4项,则![]() 的系数为
。
的系数为
。
9、设![]() ,则
,则![]() 。
。
10、下列命题中,正确命题的个数为 。
(1)两个复数不能比较大小;(2)![]() ,若
,若![]() ,则
,则![]() ;
;
(3)若![]() 是纯虚数,则实数
是纯虚数,则实数![]() ;(4)
;(4)![]() 是虚数的一个充要条件是
是虚数的一个充要条件是![]() ;(5)若
;(5)若![]() 是两个相等的实数,则
是两个相等的实数,则![]() 是纯虚数。
是纯虚数。
11、设平面内有n条直线![]() ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用![]() 表示这n条直线交点的个数,则当n>4时,
表示这n条直线交点的个数,则当n>4时,![]() =
(用含n的数学表达式表示)。
=
(用含n的数学表达式表示)。
12、设![]() ,则
,则![]() 。
。
13、如果复数![]() 满足
满足![]() ,那么
,那么![]() 的最大值是
。
的最大值是
。
14、一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是 。
二、解答题(本大题共6小题,共70分,请写出必要的解题步骤和演算过程)
15、(本题12分)计算![]()
16、(本题15分)设复数![]() 在复平面上对应点在第二、四象限的角的平分线上,
在复平面上对应点在第二、四象限的角的平分线上,![]()
![]() 的值。
的值。
17、(本题15分)袋中有4个黑球,3个白球,2个红球,从中任取2个球,每取到一个黑球得0分,每取到一个白球得1分,每取到一个红球得2分,用![]() 表示分数,求
表示分数,求![]() 的概率分布。
的概率分布。
18、(本题16分)在6名内科医生和4名外科医生中,内科主任和外科主任各一名,现要组成5人医疗小组送医下乡,依下列条件各有多少种选派方法。
(1)有3名内科医生和2名外科医生;
(2)既有内科医生,又有外科医生;
(3)至少有一名主任参加;
(4)既有主任,又有外科医生。
19、(本题16分)若![]() 展开式中前三项系数成等差数列。求
展开式中前三项系数成等差数列。求
(1)展开式中含![]() 的一次幂的项;
的一次幂的项;
(2)展开式中所有![]() 的有理项;
的有理项;
(3)展开式中系数最大的项。
20、(本题16分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 。
。
(1)试计算![]() 并猜想
并猜想![]() 的表达式;
的表达式;
(2)证明你的猜想,并求出![]() 的表达式;
的表达式;
参考答案
1、圆内不是直径的两弦,能互相平分
2、![]()
3、六
4、![]()
5、144
6、60
7、![]()
8、-6
9、![]()
10、0
11、![]()
12、129
13、![]()
14、14
15、解:原式=![]()
=![]()
=![]()
=![]()
16、解:设![]() ,则
,则![]()
因为复数![]() 在复平面上对应点在第二、四象限的角的平分线上
在复平面上对应点在第二、四象限的角的平分线上
所以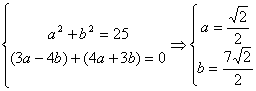 或
或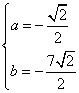
![]()
当![]() 时,
时,![]() 或
或![]()
当![]() 时,
时,![]() 或
或![]()
17、解:![]() 可能取的值为0,1,2,3,4,从袋中随机地取2个球,包含的基本事件总数为
可能取的值为0,1,2,3,4,从袋中随机地取2个球,包含的基本事件总数为![]() 。
。
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() 随机变量
随机变量![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
|
18、解:(1)120;(2)246;(3)196;(4)191
19、解:由题意得![]() ,则
,则![]() 或
或![]() (舍去)
(舍去)
(1)![]() ;
;
(2)![]() ,
,![]() ,
,![]() ;
;
(3)![]() 和
和![]() 。
。
20、解:(1)![]()
(2)利用数学归纳法证明,![]()