高二理科数学下期期中考试
数学试卷（文科） 2008-4
本试卷分填空题和解答题两部分。满分160分，考试时间120分钟。
一、填空题(本大题共14小题，每题5分，共70分)
1、已知
，
，则
。
2、化简
的结果是
。
3、已知集合
中只含有一个元素，则a的值为 。
4、如果复数
满足
，那么
的值是_________。
5、函数
的定义域为
，则
的定义域为__________。
6、已知f(x)是R上的增函数，A(0,-1),B(3,1)是其图象上的两点，那么
解是 。
7、已知
的取值范围是
。
8、当z=
时,
。
9、已知定义在R上的偶函数
在
上为增函数，且
，则满足不等式
的x范围是
。
10、若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“天一函数”，那么解析式为
，值域为{4，1}的“天一函数”共有____个。
11、在复数集上解方程：x
+8=0,结果为
。
12、若函数
的定义域为[0，
]，值域为[
]，则的取值围是 。
13、函数f(x) = (x∈R)的值域是 。
14、黑白两种颜色的正六边形地面砖按下图的规律拼成若干个图案，则第n个图案中有白色地面砖 块。
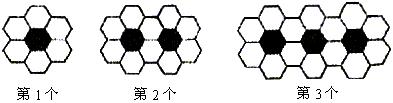
二、解答题(本大题共6小题，共90分，请写出必要的解题步骤和演算过程)
15、设集合
，
，若
，求实数a的取值范围。
16、设复数
，若
,
（Ⅰ）求实数a，b的值； （Ⅱ）若
,求
的取值范围。
17、设函数
对于
有意义，且满足条件：
，在
上为增函数。 ①证明：
；
②求
的值；
③如果
，求
的取值范围。
18、已知函数
，
（1）判断函数的奇偶性； （2）判断函数在R上的单调性，并证明；
（3）当
，合理猜想
与
的大小，不需证明。
19、已知正方形
的边长为2，有一动点
从点
出发沿正
方形的边运动，路线是
。 设点经过的路程
为，
的面积为
。求函数
的解析式及其定义域。
20、设函数定义在
上，对任意实数
，恒有
且当
。 （1）求证：
，且当
时，
；
（2）求证：在上递减； （3）设集合
，
，若
，求
的取值范围。
参考答案
1、
2、
3、0或1
4、
5、
6、
7、
8、
9、
10、9个
11、
12、
13、
14、4n+2
15、由题意,
，
且
16、解：
=1－i。(1) a=－3,b=4 ；(2)的取值范围
17、 ①令x=y=1 由f(xy)=f(x)+f(y) 得f(1)=
②x=y=2由f(xy)=f(x)+f(y) 得f(4)= f(2)+ f(2)=2
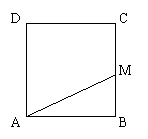
③由f(x)+ f(x－3)≤2 得f(x(x-3))≤f(4)
∴
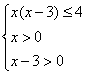得 3<x≤4
18、(1)定义域为R
则为奇函数.
(2)f(x)在R上为增函数
(3)猜想当
时，
；
时,
。
19、
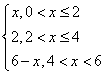定义域为
20、解：（1）证明：在f（m+n）=f（m）f（n）中，
令m=1，n=0，得f（1）=f（1）f（0）.
∵0＜f（1）＜1，∴f（0）=1.
设x＜0，则－x＞0.令m=x，n=－x，代入条件式有f（0）=f（x）·f（－x），而f（0）=1，∴f（x）=
＞1.
（2）证明：设x1＜x2，则x2－x1＞0，∴0＜f（x2－x1）＜1.
令m=x1，m+n=x2，则n=x2－x1，代入条件式，得f（x2）=f（x1）·f（x2－x1），
即0＜
＜1.∴f（x2）＜f（x1）.
∴f（x）在R上单调递减.
（3）解：由
又由（2）知f（x）为R上的减函数，∴
点集A表示圆的内部.由f（ax－y+2）=1得ax－y+2=0点集B表示直线ax－y+2=0.
∵A∩B=
，∴直线ax－y+2=0与圆
相离或相切。
于是
。