高二理科数学下检测卷(七)
高二数学组 2014-05-13
一、选择题(每小题5分,共60分)
1. ![]() 的展开式中,常数项为
的展开式中,常数项为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( )
A.5部分 B.6部分 C.7部分 D.8部分
3.顶点在同一球面上的正四棱柱![]() 中,
中,![]() ,则
,则![]() 两点间的球面距离为( )
两点间的球面距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 给出下列四个命题:
①垂直于同一直线的两条直线互相平行;②垂直于同一平面的两个平面互相平行;③若直线![]() 与同一平面所成的角相等,则
与同一平面所成的角相等,则![]() 互相平行;④若直线
互相平行;④若直线![]() 是异面直线,则与
是异面直线,则与![]() 都相交的两条直线是异面直线.其中假命题的个数是( )
都相交的两条直线是异面直线.其中假命题的个数是( )
A.4 B.3 C.2 D.1
5.已知平面![]() ,直线
,直线![]() ,直线
,直线![]() ,点
,点![]() ,点
,点![]() ,记点
,记点![]() 之间的距离为
之间的距离为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,直线
,直线![]() 和
和![]() 的距离为
的距离为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
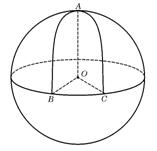 6.设球
6.设球![]() 的半径是1,
的半径是1,![]() 、
、![]() 、
、![]() 是球面上三点,已知
是球面上三点,已知![]() 到
到![]() 、
、
![]() 两点的球面距离都是
两点的球面距离都是![]() ,且二面角
,且二面角![]() 的大小是
的大小是![]() ,则
,则
从![]() 点沿球面经
点沿球面经![]() 、
、![]() 两点再回到
两点再回到![]() 点的最短距离是( )
点的最短距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() 展开式的二项式系数之和为64,则展开式
展开式的二项式系数之和为64,则展开式
的常数项为( )
A.10 B.
8.某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有( )
A.16种 B.36种 C.42种 D.60种
9.从5张100元,3张200元,2张300元的奥运预赛门票中任取3张,则所
取3张中至少有2张价格相同的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.连掷两次骰子得到的点数分别为![]() 和
和![]() ,记向量
,记向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,则
,则![]() 的概率是( )
的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.位于坐标原点的一个质点![]() 按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是
按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是![]() 。质点
。质点![]() 移动五次后位于点
移动五次后位于点![]() 的概率是( )
的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题5分,共20分)
13.一个正四棱柱的各个顶点在一个直径为![]() .
.
14.某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有 种.(用数字作答)
15.将数字1,2,3,4,5,6拼成一列,记第![]() 个数为
个数为![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则不同的排列方法有 种(用数字作答).
,则不同的排列方法有 种(用数字作答).
16.已知点![]() 在二面角
在二面角![]() 的棱上,点
的棱上,点![]() 在
在![]() 内,且
内,且![]() .若对于
.若对于![]() 内异于
内异于![]() 的任意一点
的任意一点![]() ,都有
,都有![]() ,则二面角
,则二面角![]() 的大小是
的大小是
三、解答题(第17小题10分,共余每小题12分,共70分)
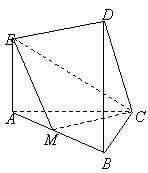 17.在如图所示的几何体中,
17.在如图所示的几何体中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求证:![]() ;(2)求
;(2)求![]() 与平面
与平面![]() 所成的角.
所成的角.
18.用0,1,2,3,4,5这六个数字 (1)组成多少个无重复数字的五位奇数?
(2)可组成多少个无重复数字的能被5整除的五位数? (3)可组成多少个无重复数字的且大于31250的五位数?
19.甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球.现从甲、乙两袋中各任取2个球 (1)若n=3,求取到的4个球全是红球概率; (2)若取到的4个球中至少有2个红球的概率为![]() ,求n.
,求n.
20.某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”则该课程考核“合格”,甲、乙、丙三人在理论考核中合格的概率分别为![]() ;在实验考核中合格的概率分别为
;在实验考核中合格的概率分别为![]() ,所有考核是否合格相互之间没有影响. (1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
,所有考核是否合格相互之间没有影响. (1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三人该课程考核都合格的概率.(结果保留三位小数)
21.某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须进行整改.若整改后经复查仍不合格,则强行关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5, 整改后安检合格的概率是0.8,计算(结果精确到0.01): (1)恰好有两家煤矿必须整改的概率; (2)至少关闭一家煤矿的概率.
22.如图,已知![]() 是棱长为3的正方体,点
是棱长为3的正方体,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() , (1)求证:
, (1)求证:![]() 四点共面;(4分)
四点共面;(4分)
(2)若点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() 面
面![]() ;(4分)
;(4分)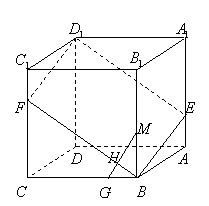 (3)用
(3)用![]() 表示截面
表示截面![]() 和
和
面![]() 所成锐二面角大小,求
所成锐二面角大小,求![]() 。(4分)
。(4分)
1~6 DCBADC 7~12 BDCACB
13.2+4![]()
14.240
15.30
16.90°
17.(1)略 (2)45°
18.(1)![]()
(2)![]()
(3)![]()
19.(1)![]() (2)
(2)![]()
20.(1)0.902 (2)0.254
21.(1)0.31 (2)0.41
22.(1)略
(2)略
(3)![]()