高二理科数学第二学期半期考试题
高二数学试题（理科）
第Ⅰ卷
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3
至4页．考试结束后，将第Ⅱ卷交回．满分150分，考试时间120分钟．
注意事项：
1． 答题前，考生务必用黑色碳素笔将自己的姓名、准考证号或座位号在答题卡上填写清
2． 把答案写在第Ⅱ卷规定位置。
一、 选择题：（共12题每题5分，共60分）
1. 复数z=2-3i对应的点z在复数平面的 （ ）
A．第一象限 B.第二象限 C.第三象限 D.第四象限
2.
已知
等于
（ ）
3.
因指数函数
是增函数（大前提）,而
是指数函数（小前提），所以是增函数（结论）”，上面推理的错误是
（ ）
（A）大前提错导致结论错 （B）小前提错导致结论错
（C）推理形式错导致结论错 （D）大前提和小前提都错导致结论错
4.
在4次独立试验中，事件A发生的概率相同，若事件A至少发生1次的概率为
，则事件A在1次独立试验中出现的概率为 （
）
A．
B．
C．
D．以上全不对
5.
若
，那么
的值是 ( )
A.1 B.
C. 
D. 
6. 五个数字0,1,2,3,4组成五位数，其中0与4不相邻的五位数共有（ ）
A．48个 B．54个 C．60个 D．66个
7. 曲线
与坐标轴围成的面积
（ ）
A.-1
B
D.3
8.
函数
的单调递减区间是
（ ）
A.（
，+∞） B.（－∞，） C.（0，） D.（e，+∞）
9. 方程x3－6x2+9x－10=0的实根个数是 ( )
A．3
B．
10.
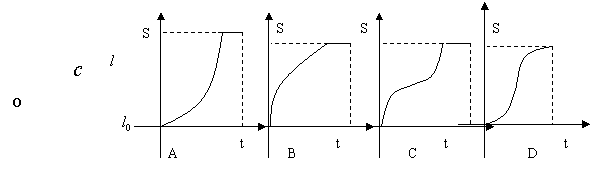已知直线
与抛物线
,当直线
从
开始在平面上绕
点按逆时针方向匀速旋转（旋转的角度不超过
）时,它扫过的面积
是时间
的函数,则函数图象大致是（ ）
11.某旅行社有
名导游，会英语的有3人，会日语的有5人，现从中选2人，只会英语或只会日语的有15种选法，则为
（ ）
A
5
B
12. 给出以下命题：
（1）若
（a＜b＝，则
；
（2）演绎推理是由一般到特殊的推理；
（3）否定结论“至多有两个解”，可以用“至少有两个解”
（4）f(x)的原函数为F(x)，且F(x)是以T为周期的函数，则
；
（5）用数学归纳法证明“
”对于
第一步证明中的
起始值
。 其中正确命题的个数为 （
）
A．1
B．
二、填空题：（本大题共4小题，每小题4分，共16分。把答案填在Ⅱ卷中的横线上）
13.计算定积分：
=
。
14. 某市区对口支援西部贫困山区教育，市区5名教师到山区3所学校支援，每校至少一人，则有 种支教方案.
15. 曲线S：
的过点A（2，-2）的切线的方程是
。
16．将侧棱相互垂直的三棱锥称“直角三棱锥”，三棱锥的侧面和底面分别叫作直角三棱锥的“直角面和斜面”；过三棱锥的顶点及斜面任何两边中点的截面均称为斜面的“中面”. 对于直角三角形有以下性质：①斜边的中线长等于斜边边长的一半；②两条直角边边长的平方和等于斜边边长的平方；③斜边与两条直角边所成的角的余弦平方和等于1. 某同学类比上述性质得到直角三棱锥的一些性质为：①斜面的中面面积等于斜面面积的四分之一；②三个直角面面积的平方和等于斜面面积的平方；③斜面与三个直角面所成二面角的余弦平方和等于1. 你认为上述性质比较恰当的是：
（写上序号）。
三、解答题（本大题共6小题，共74分，解答写出文字说明、证明过程或演算步骤）
17、（本小题满分12分）
已知
的展开式中第2项的二项式系数与第3项的二项式系数
之比为1：7.
（Ⅰ）、求n的值；
（Ⅱ）、求展开式中常数项为第几项；
（Ⅲ），求有理项的共有多少项。
18. （本小题满分12分）
已知
是二次函数，方程
有两相等实根，且
(Ⅰ)求
的解析式．
(Ⅱ）求函数与函数
所围成的图形的面积。
19．（本小题满分12分）
甲乙两人各进行一次射击，若甲乙两人击中目标的概率分别为
，
。
求下列事件的概率：
（Ⅰ）甲乙两人都击中目标。
（Ⅱ）至少有一人击中目标。
（Ⅲ）恰有一人击中目标
20． （本小题满分12分）
已知函数
= 
在x＝1处取得极值2．
（Ⅰ）求函数的解析式；
（Ⅱ）实数
满足什么条件时，函数在区间
上单调递增？
21． （本小题满分14分）
等差数列
的前项和为
．(
是虚数单位)
（Ⅰ）求数列的通项
与前项和
；
（Ⅱ）设
，求证：数列
中任意不同的三项都不可能成为等比数列．
22．（本小题满分12分）
函数对任意实数
都有
,
（Ⅰ）求
的值；
（Ⅱ）求
的值，猜想
的表达式并用数学归纳法证明你的结论；
（Ⅲ）若数列{
}，(n∈N
)是等差数列,则有数列{
}（b=
）
(n∈N)也是等差数列，类比上述性质，相应地：若数列{c}是等比数列,且
c＞0(n∈N)，则有{
}（d
）(n∈N)
也是等比数列．又类比上述性质，相应地：若数列{
}，(n∈N)是“”数列,
则有数列{
} (n∈N)也是“”数列.
写出一个数列 。