高二数学第二学期期中考试试题
高二数 学(理科)
命题人:郭朝宏 审题人:彭成江
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共40分)
注意:
1.选择题答案要用铅笔在答题卡指定位置上填涂;
2.填空及解答题用黑色钢笔或签字笔在答题卷上指定位置作答.
一、选择题:(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.一个物体的运动方程为![]() 其中
其中![]() 的单位是米,
的单位是米,![]() 的单位是秒,那么物体在
的单位是秒,那么物体在![]() 秒末的瞬时速度是( )
秒末的瞬时速度是( )
(A)![]() 米/秒 (B)
米/秒 (B)![]() 米/秒 (C)
米/秒 (C)![]() 米/秒 (D)
米/秒 (D)![]() 米/秒
米/秒
2.若复数![]() 是纯虚数(
是纯虚数(![]() 是虚数单位,
是虚数单位,![]() 是实数),则
是实数),则![]() ( )
( )
(A)2 (B)![]() (C)
(C)![]() (D)
(D)![]()
3.有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线
∥直线![]() ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为
(A)大前提错误 (B)小前提错误 (C)推理形式错误 (D)非以上错误
4.若![]() 则
则![]() =( )
=( )
(A)6 (B) 4 (C) 3 (D).2
5.![]() ( )
( )
(A)第一象限 (B) 第二象限 (C)第三象限 (D)第四象限
6.曲线![]() 上的点到直线
上的点到直线![]() 的最短距离是(
)
的最短距离是(
)
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
|
7.利用数学归纳法证明“(n+1)(n+2)(n+3)…(n+n)=2n×1×3×…(2n-1)(n∈N*)”时,从n=k变到“n=k+
(A)2k+1 (B)![]() (C)
(C)![]() (D)
(D)![]()
8.已知二次函数![]() ,对于任意实数x,有
,对于任意实数x,有![]() 的最小值为(
)
的最小值为(
)
(A) ![]() (B)
(B)![]() (C)
3 (D)
2
(C)
3 (D)
2
第Ⅱ卷(非选择题,共110分)
二、填空题: 本大题共6小题,每小题5分,共30分,把答案填在答题卷中相应横线上.
9. 曲线![]() 在点P(-1,3)处的切线方程为
.
在点P(-1,3)处的切线方程为
.
10. 图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第![]() 个图形包含
个图形包含![]() 个“福娃迎迎”,则
个“福娃迎迎”,则![]() ;
;![]() = 。(答案用数字或
= 。(答案用数字或![]() 的解析式表示)
的解析式表示)

|
11.设数函![]() 。若
。若![]() 是奇函数,则
是奇函数,则![]() _________。
_________。
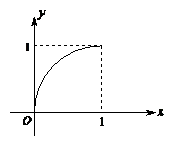 12.已知定义在区间
12.已知定义在区间![]() 上的函数
上的函数![]() 的图像如图所示,对于满足
的图像如图所示,对于满足![]() 的任意
的任意![]() 、
、![]() ,给出下列结论:
,给出下列结论:
![]() ;
;
![]() ;
;
![]() .
.
其中正确结论的序号是 .(把所有正确结论的序号都填上)
13.已知![]() ,则
,则![]() 的最大值是
.
的最大值是
.
14.在![]() 中,两直角边分别为
中,两直角边分别为![]() 、
、![]() ,设
,设![]() 为斜边上的高,则
为斜边上的高,则![]() ,由此类比:三棱锥
,由此类比:三棱锥![]() 中的三条侧棱
中的三条侧棱![]() 、
、![]() 、
、![]() 两两垂直,且长度分别为
两两垂直,且长度分别为![]() 、
、![]() 、
、![]() ,设棱锥底面
,设棱锥底面![]() 上的高为
上的高为![]() ,则 。
,则 。
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤 , 把答案写在答题卷上指定位置处 .
15.已知![]() ,其中
,其中![]() 是
是![]() 的共轭复数,求复数
的共轭复数,求复数![]() .
.
16.求由![]() 与直线
与直线![]() 所围成图形的面积.
所围成图形的面积.
17.函数![]() 对任意实数
对任意实数![]() 都有
都有![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值,猜想
的值,猜想![]() 的表达式并用数学归纳法证明你的结论;
的表达式并用数学归纳法证明你的结论;![]()
|
18.已知a、b为实数,且b>a>e,其中e为自然对数的底,求证:![]() .(提示:可考虑用分析法找思路)
.(提示:可考虑用分析法找思路)
19.一物体按规律![]() 作直线运动,式中x为时间t内通过的距离,媒质的阻力正比于速度的平方.试求物体由x=0运动到x=a时,阻力所作的功.
作直线运动,式中x为时间t内通过的距离,媒质的阻力正比于速度的平方.试求物体由x=0运动到x=a时,阻力所作的功.
20.已知函数![]() 为实常数.
为实常数.
(1)、a在什么范围内时,![]() 只有一个公共点?
只有一个公共点?
(2)、若![]() 上有最小值2,求a的值.
上有最小值2,求a的值.
|
|
 南雄中学2007-2008学年第二学期期中考试答题卷
南雄中学2007-2008学年第二学期期中考试答题卷
高二数 学(理科)
注意事项:
1.用黑色钢笔或黑色签字笔答在指定位置处.
2.答卷前将密封线内的项目填写清楚.
二、填空题:(30分)
9.______________. 10.____________.
11._______________. 12.__________________.
13、 ; 14、 。
三、解答题:(共6小题,80分.解答应写出文字说明,证明过程或演算步骤.)
15.(12分)
_16. 16。(12分)
.
|
|
18. (14分)
|
19(14分)
|
20. (14分)
|
高二数 学(理科)答案及评分标准
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | C | A | D | B | A | C | D |
二、填空题
9.![]() ;10.41;
;10.41;![]() ;11.
;11.![]()
12.2,3;13.![]() ,;14.
,;14.![]()
三、解答题
15解:由已知得 ![]()
设![]() ,代入上式得
,代入上式得![]()
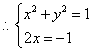 ,解得
,解得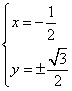
故复数![]() 为
为![]() 分
分
 16、解:由
16、解:由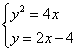 得交点坐标为
得交点坐标为![]() ,如图
,如图
(或答横坐标)
方法一:阴影部分的面积
![]()
![]()
![]()
方法二:阴影部分的面积 ![]()
![]() = 9
= 9
方法三:直线与![]() 轴交点为(2,0)所以阴影部分的面积
轴交点为(2,0)所以阴影部分的面积
![]()
![]() = 9
= 9
17. 解:(Ⅰ)
令![]() ,得
,得
![]() ……
……
证明:(Ⅱ)![]() ,
,
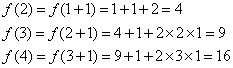
猜想![]() ,下用数学归纳法证明之.
,下用数学归纳法证明之.
(1)当n=1时,f(1)=1,猜想成立;
(2)假设当n=k时,猜想成立,即 ![]() ,
,
则当n=k+1时, f(k+1)=f(k)+f(1)+2k×1=k2+2k+1=(k+1)2
即当n=k+1时猜想成立。
由(1)、(2)可知,对于一切n∈N*猜想均成立。
18.证法一:∵b>a>e,∴要证![]() ,只要证blna>alnb,设f(b)=blna-alnb(b>e),则
,只要证blna>alnb,设f(b)=blna-alnb(b>e),则
f′(b)=lna-![]() .∵b>a>e,∴lna>1,且
.∵b>a>e,∴lna>1,且![]() <1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴
<1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴![]() .
.
证法二:要证![]() ,只要证blna>alnb(e<a<b
,只要证blna>alnb(e<a<b![]() ,即证
,即证![]() ,设f(x)=
,设f(x)=![]() (x>e),则f′(x)=
(x>e),则f′(x)=![]() <0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
<0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
∴f(a)>f(b),即![]() ,∴
,∴![]() .
.
19解:物体的速度![]() .媒质阻力
.媒质阻力![]() ,其中k为比例常数,k>0.
,其中k为比例常数,k>0.
当x=0时,t=0;当x=a时,![]() ,又ds=vdt,故阻力所作的功为
,又ds=vdt,故阻力所作的功为
![]()
20.解:已知函数![]() 为实常数.
为实常数.
(1)a在什么范围内时,![]() 只有一个公共点?
只有一个公共点?
(2)若![]() 上有最小值2,求a的值.
上有最小值2,求a的值.
【解析】(1)![]() .
.
①当![]() 时,
时,![]() ,所以
,所以![]() 在R上单调增,此时
在R上单调增,此时![]() 只有一个公共点;
只有一个公共点;
②当![]() 时,
时,![]() .由
.由![]() ,得
,得![]() .
.
在![]() 上列表:
上列表:
|
|
|
|
|
|
|
|
| + | 0 | ─ | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
因为![]() 只有一个公共点,所以
只有一个公共点,所以![]() 或
或![]() .
.
所以![]() ,得
,得![]() .
.
综上,![]() ,
,![]() 只有一个公共点.
只有一个公共点.
(2)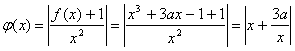 .
.
由![]() ,可知
,可知![]() 为偶函数,则原题即为
为偶函数,则原题即为![]() 在
在![]() 上有最小值2.
上有最小值2.
设![]() (
(![]() ),则
),则![]() .
.
①![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调增,所以
上单调增,所以![]() .
.
因为![]() 在
在![]() 上有最小值2,所以
上有最小值2,所以![]() ,所以
,所以![]() .
.
②![]() 时,
时,![]() ,无最小值,不合题意.
,无最小值,不合题意.
③![]() 时,
时,![]() ,
,![]() .
.
(I)![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]() ,此时
,此时![]() 在
在![]() 上的最小值为
上的最小值为![]() ,不合题.
,不合题.
(II)![]() ,即
,即![]() 时,由
时,由![]() ,得
,得![]() .
.
在![]() 上列表:
上列表:
|
|
|
|
| 2 |
|
| ─ | 0 | + | |
|
| ↘ | 极小值 | ↗ |
|
∴![]() ,即
,即![]() .综上,
.综上,![]() 的值为
的值为![]() .
.