高二数学第二学期期中联考试卷
（高二数学）
（考试时间120分钟 试卷满分160分）
一、填空题：本大题共7小题，每小题5分，共35分。把答案填在答题卡相应位置
1、设A=
B=
若B
A，且B中至少有两个偶数，则这样的集合B的个数为
2、现给出一个的算法的算法语句如右图：此算法的运
行结果是_____；
3、完成下面的三段论：
大前提：互为共轭复数的乘积是实数
小前提：
与
是互为共轭复数
结 论：
4、在等差数列
中，已知
，则
的值为_____.
5、用反证法证明命题“如果
那么
”时，假设的内容应为__________.
6、已知一个样本1，2，3，5，x的平均数为3，则这个样本的标准差s=_______
7、命题“对任意的
”的否定是
8、一只蚂蚁在边长为3的正方形区域内随机地爬行,则
其恰在离四个顶点距离都大于1的地方的概率
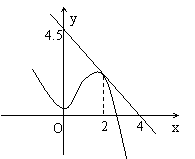
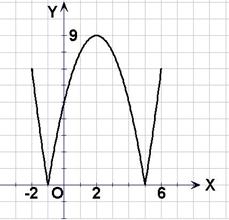
9、如右图所示，函数
的图象在点P处的
切线是直线
10、如果复数
是实数，则实数
。
11、若关于x的不等式
的解集为（1,2），则关于x不等式
的解集为___________；
12、若
的最小值是_______.
13、已知双曲线
的左、右焦点分别为
，
，
是准线上一点，且
，
，则双曲线的离心率为 ．
14、下面是按照一定规律画出的一列“树型”图：
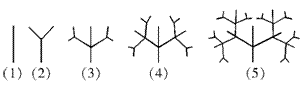
设第
个图有
个树枝，则
与
之间的关系是______
．
07－08学年楚天外国语学校第二学期高二数学期中试卷答题卡
（考试时间120分钟 试卷满分160分）
一、填空题：本大题共14小题，每小题5分，共70分。把答案填在答题卡相应位置
1.__________________ 2.__________________ 3._________________
4.__________________ 5.__________________ 6._________________
7.__________________ 8.__________________ 9._________________
10._________________ 11._________________ 12.________________
13._________________ 14._________________
二、解答题：本大题共6小题,共90分。解答应写出文字说明、证明过程及演算步骤。
15、（14分）已知
为复数，
.
16、（14分）某单位决定投资3200元建一个形状为长方体的仓库，高度一定，它的后墙利用旧墙不用花钱，正面用铁栅，每米造价为40元，两侧墙砌砖，每米造价45元，屋顶每平方米造价20元，设铁栅的长为x米，两侧墙各为y米，
（1）试写出x,y满足的条件；
（2）仓库面积S的最大允许值是多少平方米？
17、（14分）（1）已知椭圆中心在原点，焦点在
轴，长轴长为短轴长的3倍，且过点
，求此椭圆的方程；
（2）求与双曲线
有公共渐近线，且焦距为8的双曲线的方程．
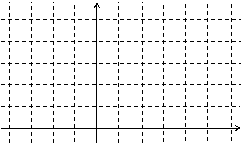
18．(16分) 设函数
.
（1）在区间
上画出函数
的图像；
（2）设集合
. 试判断集合
和
之间的关系；
（3）当
时，求证：在区间
上，
的图像位于函数图像的上方.
 |
19、（16分）已知函数
的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为
.
（Ⅰ）求函数的解析式；
（Ⅱ）求函数的单调区间.
20、（16分）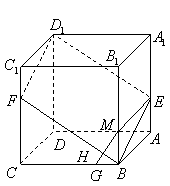
如图，已知
是棱长为
的正方体，点
在
上，点
在
上，且
．
（1）求证：
四点共面；
（2）若点
在
上，
，点
在
上，
，垂足为
，求证：
平面
；
（3）用
表示截面
和侧面所成的锐二
面角的大小，求
．
高二数学参考答案
说明：
1．本解答仅给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制订相应的评分细则．
2．评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误时，如果后继部分解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．给分或扣分均以1分为单位，填空题不给中间分．
一、填空题：本大题共14小题，每小题5分，共70分。把答案填在答题卡相应位置
1.60 2.11 3. 
是实数 4.30 5. 
6. 
7. 
8. 
9. 9/8 10. －1
11. 
12. 3 13. 
14. an+1=2an+1
二、解答题：本大题共6小题,共90分。解答应写出文字说明、证明过程及演算步骤。
15、（14分）已知为复数，.
解：设
则
为纯虚数
……………………………………6分
于是x=3y 
∴y=5 即y=±5 …………………………………………12分
故
…………………………14分
16、（14分）某单位决定投资3200元建一个形状为长方体的仓库，高度一定，它的后墙利用旧墙不用花钱，正面用铁栅，每米造价为40元，两侧墙砌砖，每米造价45元，屋顶每平方米造价20元，设铁栅的长为x米，两侧墙各为y米，
（1）试写出x,y满足的条件；
（2）仓库面积S的最大允许值是多少平方米？
解：
（1）依题意，S=xy，且x>0,y>0，40x+90y+20xy=3200即4x+9y+2xy=320,
所以x,y满足的条件是4x+9y+2xy=320,x>0,y>0.
(2)
方法1：（代入消去x）由4x+9y+2xy=320得到，
，设t=y+2，∵x,y>0，∴0<y<
,
( 当且仅当t=
时，等号成立)
∴S=
∴当t=，即
，x=15时，S取得最大值100；
17、（14分）（1）已知椭圆中心在原点，焦点在轴，长轴长为短轴长的3倍，且过点，求此椭圆的方程；
（2）求与双曲线有公共渐近线，且焦距为8的双曲线的方程．
解：
（1）
；
…………5分
（2）
．
…………10分
18．(16分) 设函数.
（1）在区间上画出函数的图像；
（2）设集合. 试判断集合和之间的关系；
（3）当时，求证：在区间上，的图像位于函数图像的上方.
[解]（1）
……5分
（2）方程
的解分别是
和
，由于在
和
上单调递减，在
和
上单调递增，因此
.
……8分
由于
.
……10分
（3） 当
时，
.
，
……12分
. 又
，
① 当
，即
时，取
，
.
，
则
.
② 当
，即
时，取
， ＝
.
由 ①、②可知，当时，
，.
因此，在区间上，
的图像位于函数图像的上方. ……16分
19、（16分）已知函数的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为.
（Ⅰ）求函数的解析式；
（Ⅱ）求函数的单调区间.
解：（Ⅰ）由
的图象经过P（0，2），知d=2，所以
……3分
由在
处的切线方程是，知
故所求的解析式是 
……8分
（Ⅱ）
解得 
……10分
当
当
故
内是增函数，在
内是减函数，
在
内是增函数.
……16分
20、（16分）如图，已知是棱长为的正方体，点在上，点在上，且．
（1）求证：四点共面；
（2）若点在上，，点在上，
，垂足为，求证：平面；
（3）用表示截面和侧面所成的锐二
面角的大小，求．
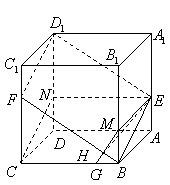解法一：
（1）如图，在
上取点
，使
，连结
，
，则
，
．
因为
，
，所以四边形
，
都为平行四边形．
从而
，
．
又因为
，所以
，故四边形
是平行四边形，由此推知
，从而
．
因此，四点共面．
（2）如图，，又
，所以
，
．
因为
，所以
为平行四边形，从而
．
又
平面，所以平面．
（3）如图，连结
．
因为
，
，所以
平面
，得
．
于是
是所求的二面角的平面角，即
．
因为
，所以
，
．
解法二：
（1）建立如图所示的坐标系，则
，
，
，
所以
，故
，
，
共面．
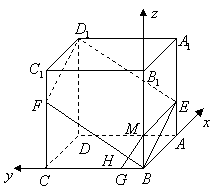又它们有公共点
，所以四点共面．
（2）如图，设
，则
，
而，由题设得
，
得
．
因为
，
，有
，
又
，
，所以
，
，从而
，
．
故
平面．
（3）设向量
截面，于是
，
．
而，，得
，
，解得
，
，所以
．
又
平面，所以
和
的夹角等于或
（为锐角）．
于是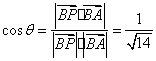
．
故
．