高二数学第二学期期中试卷
数 学 试 卷
班 姓名 学号 得分
一、选择题(每小题只有一个正确的答案，每小题3分)：
1．有下列三个命题：
命题1：
命题2：两组对边分别相等的四边形是平行四边形
命题3：一条直线与一个平面的无数条直线垂直，则此直线垂直于该平面
其中正确命题的个数是 ( )
A. 0 B.
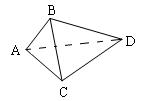2．设A、B、C、D是空间四个不同的点，在下列命题中，不正确的是（ ）
（A）若AC与BD共面，则AD与BC共面
（B）若AC与BD是异面直线，则AD与BC是异面直线
(C) 若AB=AC，DB=DC，则AD=BC
(D) 若AB=AC，DB=DC，则AD ⊥BC
3．已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，
下列四个命题中正确的是 （ ）
A．若
；
B．若l⊥β且α⊥β,则l∥α；
C．若
；
D．若m、n是异面直线，
4．在
中，已知ÐB=90°，ÐC=30°，AC=4,D是BC中点，E是平面ABC外一点， DE^平面ABC, DE=1，那么点E到直线AC的距离为
（ ）
A.
B. 
C. 
D.2
5．一个正方体内接于一个球，过球心作一截面，则截面的可能图形是 （ ）
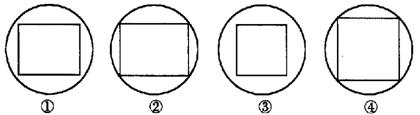
A. ①③ B. ②④ C. ①②③ D. ②③④
二、填空题Ⅰ（每小题3分）：
6．一个六棱柱的底面是边长为a的正六边形，侧棱长为b，侧棱与底面所成的角为60°，则这个棱柱的体积为
7． A、B、C是球O表面上三点，AB=6,BC=8，AC=10，点O到△ABC所在平面的距离为5，则球O的表面积为 。
8．在一个坡面的倾斜角为60°的斜坡上，有一条与坡脚的水平线成30°角的直线，沿这条道行走到
9．已知半径为R的球面上有两点A、B，且AB=
，则这两点的球面距离为
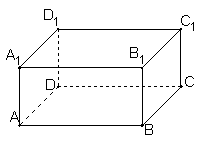10.如图所示，以长方体ABCD—A1B
（注：只写出其中一个并在图中画出相应的四面体）。
三、填空题Ⅱ（每小题2分）：
1．函数
的定义域为
2．若点A(1,2)既在函数
=
的图象上，又在的反函数的图象上，则a的值为
.
3.点(2,1)到直线3x-4y+2=0的距离是
4．已知cos
=
，则cosα的值为
5．某校一个数学研究性学习小组共有8个同学，其中男同学5人，女同学3人
现从这8个同学中选出3人准备一个报告会，要求在选出的3人中男
女同学都有，则不同的选法共有
种（用数字作答）
6
“
”是“
”的（ ）
A
充要条件 B
充分不必要条件 C
必要不充分条件 D
既不充分又不必要条件
7．在等差数列
中
，那么前n项的和
等于
8．已知
=（3，4），
=（x，－1），⊥，则x的值为
9．双曲线
的离心率为
10．数列｛an｝的前n项和为Sn＝n2-n+2，则该数列的通项公式为 .
四、解答题（答题要求：请写出规范的完整的解答过程）：
1．（12分）如图, 在直三棱柱ABC－A1B
ACB=90°，AC＝2，BC＝2，AA1＝4，点D是AB的中点，
（I）求证：平面CDB1⊥平面ABB
（II）求异面直线 AC1与 B
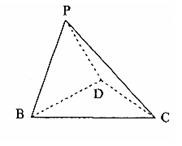
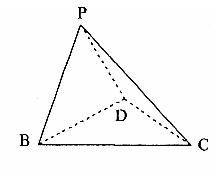2．（12分）已知三棱锥P—BCD中，PD=PB，
，BD=CD，∠BDC=90°，
平面
。
（I）求证：
；
（II）求直线BC与平面PDC所成的角的大小。
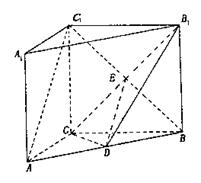
3．（14分）如图，ABCD—A1B
（I）求证：BD1∥平面C1DE；
（II）求二面角C1—DE—C的大小；
（III）在侧棱BB1上是否存在点P，
使得CP⊥平面C1DE？证明你的结论.
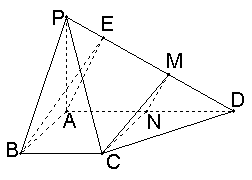
4．（12分）在四棱锥P—ABCD中，底面ABCD是一直角梯形，
，
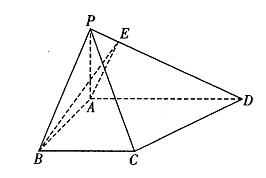（1）若
为垂足，
求证：
；
（2）求点A到平面PBC的距离。
| |
附加题（本题共10分，计入总分，但总分不超过100分）：
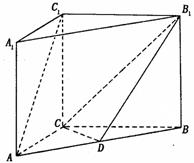
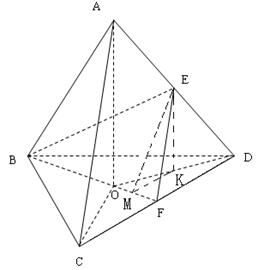
如图，棱长为1的正四面体ABCD中，E、F分别是棱AD、CD的中点，O是点A在平面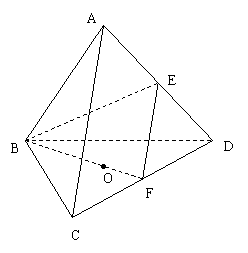
BCD内的射影.
(I)求点O到平面ACD的距离；
(Ⅱ) 求二面角E-BF-D的大小.
高二年级期中
数 学 试 卷 参 考 答 案
一、选择题（每小题3分）：1.A 2.C 3.D 4.A 5.C
二、填空题Ⅰ（每小题3分）：6．
7．
8．
9．
10．略
三、填空题Ⅱ（每小题2分）：
1．
2．－3 3．
4．
5．45
6．B
7．
8．
9．
10．
（没有n的范围，或者只写出一种情况，给零分）
四、解答题：
1．（本题满分12分）
（I）证明：直三棱柱ABC－A1B
∴BB1⊥CD…………………………1分
∵AC＝BC＝2，D是AB的中点
∴ CD⊥AB…………………………2分
∵BB1 ∩AB=B
∴CD⊥平面ABB
∵CD
平面CDB1
∴平面CDB1⊥平面ABB
（II）解：连结BC，交BC于E，连结DE
∵ D是AB的中点，E是BC1的中点，
∴ DE//AC1，
∴ ∠CED或其补角为AC1与B
在△CED中，ED=
AC 1=，CD=AB=
，CE=CB1=，
∴由余弦定理得 
，…………………………11分
∴ 异面直线 AC1与 B.…………………………12分
注：若用向量法得到结论
，扣1分；若用向量法得到非
的数值，给零分。
2．（本题满分12分）
解：（I）
…………………………4分
…………………………6分
（II）∵CD⊥BP，BP⊥PD，PD ∩CD=D
∴BP⊥面PDC
∴BC与平面PDC所成的角为∠BCP…………………………9分
设BP=
，则BD=
，
在
BCP中， BP=，BC=2
∴∠BCP=30°…………………………11分
∴所求的角为30°…………………………12分
注：若用向量法得到结论
，
，
，扣2分；若用向量法得到其它错误的结论，给零分。
3．（本题满分14分）
（I）证明：连接CD1，与C1D相交于O，连接EO.
∵CDD
∴O是CD1的中点，
又E是BC的中点，
∴EO∥BD1.………………2分
又BD1
平面C1DE，EO平面C1DE，
∴BD1∥平面C1DE.……………………………4分
（II）解：过点C作CH⊥DE于H，连接C1H.
在正四棱柱ABCD—A1B
CC1⊥平面ABCD，
∴C1H⊥DE，
∠C1HC是二面角C1—DE—C的平面角.…………7分
根据平面几何知识，DE=，CH=
………………9分
∴二面角C1—DE—C的大小为 
………………10分
注：若用向量法得到结论
，扣1分；若用向量法得到其它错误的结论，给零分。
（III）解：在侧棱BB1上不存在点P，使得CP⊥平面C1DE……………………11分
证明如下：
假设CP⊥平面C1DE，则必有CP⊥DE.
而PC在平面ABCD内射影为BC，则必有BC⊥DE.
这与已知点E是BC的中点相矛盾
∴假设CP⊥平面C1DE不成立，
即在侧棱BB1上不存在点P，使得CP⊥平面C1DE.………………………14分
4．（本题满分12分）
解：（1）
…………………………4分
（2）设A到平面PBC的距离为h
AB⊥BC
∴由三垂线定理得 PB⊥BC
∵
∴
∴ 
即所求为
…………8分
注：若用向量法得到错误结论，给零分。
（3）取AD中点N，连结CN，作NM⊥PD于M，连结CM
∴CN∥AB
∴ CN⊥平面PAD
∴CM⊥PD
∴∠CMN为二面角C－PD－A的平面角 …………………………10分
在△CMN中，CN=a，NM=
a
∴∠CMN=
∴所求为 …………………………12分
注：若用向量法得到结论
，扣1分；若用向量法得到其它错误的结论，给零分。
附加题（本题满分10分）：
解：
（1）如图，连结AO，CO，DO，
点O到平面ACD的距离就是三棱锥O-ACD底面ACD上的高h.
因为VO-ACD=VA-COD，…………………………1分
在正△BCD中，OF=
，AO=
，…………2分
所以VA-COD =
·(
··1)=
. …………………………3分
VO-ACD=·h·(·
·1) .
…………………………4分
解得h=
.所以所求为…………5分
(2)在正四面体ABCD，OA⊥平面ＢＣD.
设OD的中点为K，则EK∥OA.
所以ＥK⊥平面ＢＣＤ.
在面BCD内，过点K作KM∥CD，
KM交BF于M，连结EM
因为BF⊥CD，
所以KM⊥BF.
所以EM⊥BF.
所以∠EMK是所求二面角的平面角. ……8分
因为EK=AO=·=
，
MK=FD=
AD=，
所以tan∠FMK=
=
. …………………………9分
所以所求二面角的大小为arctan
. ……………………………………10分
注：若用向量法得到结论
，扣1分；若用向量法得到其它错误的结论，给零分。
注：1.用向量法解题的步骤要求：建系，写点的坐标，写向量的坐标，求法向量的坐标，求角或求距离，写结论。若用向量法答案正确但步骤不完整，请酌情扣分。若用向量法但答案不正确，依各题答案后的注解给分。
2. 若用其它的传统法解题，请酌情按步骤给分。