高二数学第二学期期中试卷
高 二 数 学 080428
一． 填空题(本题共14小题，每题5分，共70分)：
1．已知集合
，集合
，则
= .
2．函数
的定义域是
.
3．复数
的共轭复数是
.
4．回归直线方程为y=0.5x-0.81，则x=25时，y的估计值为 .
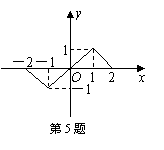5．函数
的图象如图所示，
则
＋
= .
6．已知
是偶函数，定义域为
，则
= .
7．复数
在复平面内所对应的点
位于第_____象限
8．给出数表
请在其中找出4个不同的数，使它们能构成等比数列，这4个数从小到大依次是
.
9．某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：
| 性别 专业 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
为了判断主修统计专业是否与性别有关系，根据表中的数据，得到
因为
，所以判定主修统计专业与性别有关系，那么这种判断出错的可能性为_____________.
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
10．设周期函数
是定义在R上的奇函数，若
的最小正周期为3，且
，
，则m的取值范围是
.
11．已知
，且函数
的最小正周期是
. 类比上述结论，若
，
为正的常数，且有 
，则
的最小正周期是
.
12．若函数
在区间
内有且只有一个零点，那么实数
的取值范围是
．
13．某厂家根据以往的经验得到下面有关生产销售的统计：
每生产产品
（百台），其总成本为
万元，
；销售收入
（万元）.满足：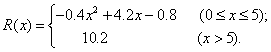 
要使工厂有赢利，产量x的取值范围是 ．
14．从
中，可得到一般规律为 ．(用数学表达式表示)
二． 解答题（共6小题，共90分，解答时应写出文字说明，证明过程或演算步骤）：
15．（本题14分）已知复数
满足
且
为实数，求
.
16．（本题14分）定义运算
，集合
，
，求：
与
．
17．（本题14分）已知
＜0，并且4x
-9y=36．由此能否确定一个函数关系？如果能，求出其解析式、定义域和值域；如果不能，请说明理由．
18．（本题16分）某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | | | | | | |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率；(6分)
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程
；(7分)
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?(3分)
(参考公式: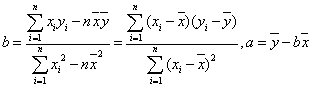 
)
19．（本题16分）已知
．
（1）证明：函数
在
上为增函数；
（2）用反证法证明：方程
没有负数根．
20．（本题16分）已知二次函数
满足：对任意实数x，都有
，且当
（1，3）时，有
成立.
（1）证明：
;
（2）若
的表达式;
（3）设
，若
图上的点都位于直线
的上方，求实数m的取值范围.
高二数学期中试卷参考答案：
一．填空题：
1．
2. 
∪
3. 
4. 11.96
5.0 6. 
7 三 8. 如2，6，18，54等
9. 5％
10. 
11. 
12. 
13. （1，8.2）
14. 
二．解答题：
15. 
16. 
∴ 
即
…………6分
∵
，∴ 
∴ 
，则
即
………10分
∴
………14分
17. 
，故
解得
，
……5分
又
……7分
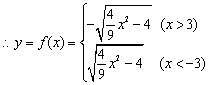……9分
因此能确定一个函数关系y=f(x)．其定义域为(-∞，-3)∪)3，+∞)．且不难得到其值域为(-∞，0)∪(0，＋∞)． ……14分
18. (Ⅰ)设抽到相邻两个月的数据为事件A.因为从6组数据中选取2组数据共有15种情况,每种情况都是等可能出现的………3分
其中,抽到相邻两个月的数据的情况有5种 …………4分
所以
…………………6分
(Ⅱ)由数据求得
………7分
由公式求得
………………10分
再由
……………………12分
所以
关于
的线性回归方程为
…………13分
(Ⅲ)当
时,
, 
； …………14分
同样, 当
时,
, 
…………15分
所以,该小组所得线性回归方程是理想的. …………16分
19. 证明：（1）
．…………4分
，
，
，………6分
，
函数在
上为增函数；……8分
（2）假设存在
，满足
，………10分
则
，
，
，………13分
解得
，与假设
矛盾．故方程
没有负数根．…16分
20. （1）由条件知 
恒成立
又∵取x=2时，
与恒成立
∴ …………4分
（2）∵
∴
∴
……6分
又 
恒成立，即
恒成立
∴
， …………10分
解出：
，∴
…………12分
（3）由分析条件知道，只要图象（在y轴右侧）总在直线 
上方即可，也就是直线的斜率
小于直线与抛物线相切时的斜率位置，于是：
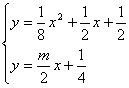利用相切时△=0，解出 
∴
…………16分