高二数学第二学期期未模拟试卷

高二数学第二学期期未模拟试卷〈一〉

参考公式（数据）：

P(c2≥x0)	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
x0	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

线性相关系数公式：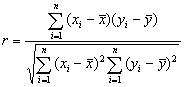

线性回归方程系数公式：，其中，．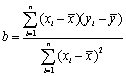

一．填空题：本大题共14小题，每小题5分，共70分，把答案填在答题卡指定位置上．

1．(x－y)¹⁰的展开式中x⁶y⁴项的系数是_____________

2．一个学生能够通过某种英语听力测试的概率是，他连续测试2次，那么其中恰有一次获得通过的概率是________

3．若复数（a∈R，i为虚数单位）是纯虚数，则实数a的值为________

4．通过随机询问250名不同性别的大学生在购买食物时是否看营养说明书，得到如下2×2联表：

	女	男	总计
读营养说明书	90	60	150
不读营养说明书	30	70	100
总计	120	130	250

从调查的结果分析，认为性别和读营养说明书的有关的可能性在___________以上。

5．抛掷一颗质地均匀的骰子，将向上一面的点数看作随机变量X，则X的方差是　　．

6．从一副不含大小王的52张扑克牌中不放回地抽取2次，每次抽1张，已知第1次抽到A，那么第2次也抽到A的概率为_______．

7．从4位男教师和3位女教师中选出3位教师，派往郊区3所学校支教，每校1人，要求这3位教师中男、女教师都要有，则不同的选派方案有___种（用数字作答）

8．若z∈C且z＋2－2i＝1，则z－2－2i的最小值等于________

9．若(2x－1)⁷＝a₇x⁷＋a₆x⁶＋…＋a₁x＋a₀，则a₇＋a₅＋a₃＋a₁＝_____________．

10.已知△ABC，A(1,1)，B(3,1)，C(3,3)，经过矩阵所对应的变换，得到的三角形面积是__________　

11.“因134682的数字之和等于24是3的倍数，故134682能被3整除”这一推理的大前提是　 　　　　　　　　　　　　　　　　　　　　．

12． 已知方程是根据女大学生的身高预报她的体重的回归方程，其中x的单位是cm，的单位是kg，那么针对某个体（160，53）的随机误差是　　  ．

13、观察下列算式，猜测由此表提供的一般法则，用适当的数学式子表示它。

	1=1 3+5=8 7+9+11=27 13+15+17+19=64 21+23+25+27+29=125 ……

则这个式子为　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

14．若A，B，C，D，E，F六个不同元素排成一列，要求A不排在两端，且B、C相邻，则不同的排法共有________种（用数字作答）

二、解答题：本大题共6小题；共90分．解答应写出文字说明、证明过程或演算步骤．

15．(本题12分)已知复数z₁满足(1+i)z­₁=－1+5i， z­₂=a－2－i，其中i为虚数单位，a∈R，若<z₁，求（1）z₁ 　　 （2）a的取值范围.

16．某电脑公司有6名产品推销员，其工作年限与年推销金额数据如下表:

推销员编号	1	2	3	4	5
工作年限/年	3	5	6	7	9
推销金额/万元	2	3	3	4	5

(Ⅰ)求年推销金额与工作年限x之间的相关系数；

(Ⅱ)求年推销金额关于工作年限的线性回归方程；

(Ⅲ)若第6名推销员的工作年限为11年，试估计他的年推销金额.

（参考数据：；由检验水平0.01及,查表得.）

17．从5名女同学和4名男同学中选出4人参加演讲比赛，分别按下列要求，各有多少种不同选法？⑴男、女同学各2名；　　⑵男、女同学分别至少有1名；

⑶在(2)的前提下，男同学甲与女同学乙不能同时选出.

18．一袋中有（）个红球,3个黑球和2个白球，现从中任取2个球．

(Ⅰ)当时,求取出的2个球球颜色都相同的事件的概率；

（Ⅱ）当时，设表示取出的2个球中红球的个数，求的概率分布及数学期望；

(Ⅲ)如果取出的2个球颜色不相同的事件概率小于，求的最小值．

19．数列满足：=1，， （）

（1）求实数的值（2）求的值，根据，，的值，猜想与的关系式，并证明你的猜想

20．(本题18分)某同学做了一个数字信号模拟传送器，经过10个环节，把由数字0,1构成的数字信号由发生端传到接受端。已知每一个环节会把1错转为0的概率为0.3，把0错转为1的概率为0.2，若发出的数字信号中共有10000个1，5000个0.

问：(1)从第1个环节转出的信号中0,1各有多少个？

　　　　(2)最终接受端收到的信号中0,1个数各是多少？(精确到十位)

　　　　(3)该同学为了完善自己的仪器，决定在接受端前加一个修正器，把得到的1和0分别以一定的概率转换为0和1，则概率分别等于多少时，才能在理论上保证最终接受到的0和1的个数与发出的信号同.

 

期未模拟试卷〈一〉参考答案及评分标准

一．填空题：1。－840　 2。　3。－6　4。99.9% 5。 6。 7。180

8。3  9。1094  10。2  11。数字之和能被3整除的正整数一定是3的倍数．

12。－0.29　　  13。　14。144

二、解答题：15。解：由题意得 z₁==2+3i，

　　  于是==，=.

　　 <，

得a²－8a+7<0，1<a<7.

所以a的取值范围是(1,7)

16.解： (Ⅰ)由=10，20，5.2，

　　 可得.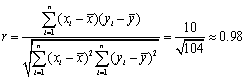

∴年推销金额与工作年限x之间的相关系数约为0.98．　　

(Ⅱ) 由(Ⅰ)知，,

　　 ∴可以认为年推销金额与工作年限x之间具有较强的线性相关关系.

设所求的线性回归方程为，

则，.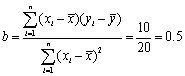

∴年推销金额关于工作年限的线性回归方程为.　

　 (Ⅲ) 由(Ⅱ) 可知,当时,

万元.

∴可以估计第6名推销员的年推销金额为5.9万元．　　　　　

17．[解]：⑴＝60　 ⑵＝120

⑶120-()＝99

答：（略）说明：若仅有如上列式，无文字说明，则每小题扣1分。

18．解: (Ⅰ) 当时,设“取出的2个球颜色都相同”为事件,

　　　

答: 取出的2球颜色都相同的事件概率为

（Ⅱ）当时,可取0、1、2，

	0	1	2

．　　　

(Ⅲ) 设“取出的2个球中颜色不相同”为事件,则

　　　  

∴，

∴或，

∴的最小值为6．　　　　　

19．（1）将a₁,a₂,a₃的值代入a_n+2= a_n+1+2a_n+t得t= - 1　 　　　　　　 

（2）a₄=a₃+2a₂ – 1=3+4 – 1=6　　　∴a₃+a₄=9　　 　　　　　　 

由于a₁+a₂=2＋１,　　a₂+a₃=2² +1,　　a₃+a₄=2³+1

猜测可得：a_n+a_n+1=2ⁿ+1 　　　　　　　　　　　　　　　　　　　

证明：n=1时，a₁+a₂=2¹+1成立

　　假设n=k时，a_k+a_k+1=2^k+1成立

　　则n=k+1时，a_k+2+a_k+1=a_k+1+2a_k+a_k+1-1=2(a_k+1+a_k)-1

　　利用归纳假设得

　　 a_k+2+a_k+1=2·(2^k+1)-1=2^k+1+1

∴　n=k+1时命题也成立

∴　对n∈N^＊有a_n+a_n+1=2ⁿ+1成立

（也可以用其他方法证明）

20。 解：(1)从第1个环节转出的信号中，0的个数为：

　　　　　　 10000×0.3+5000×0.8=7000(个)

　　　　　  1的个数为：10000×0.7+5000×0.2=8000(个)

　　　 (2)数字错转的转移矩阵为A=，1和0的个数对应列矩阵，

于是最终接受端收到的信号中1,0个数对应矩阵A¹⁰，

矩阵A的特征多项式为：

　　 ==

令=0，得到A的特征值为1或0.5，将1代入方程组

　　

解得3x－2y=0，不妨设x=2，于是得到矩阵A的属于特征值1的一个特征向量为.

同理，把λ=0.5代入上述方程组得x+y=0，不妨设x=1，可得矩阵A的属于特征值0.5的一个特征向量为.

 又设=m+n，于是，求得，

所以A¹⁰=3000·1¹⁰+4000·0.5¹⁰=

于是，最终接受端收到的信号中0约有9000个，1约有6000个

(3)设修正器的转移矩阵为B=(0<s<1, 0<t<1)，则题意有

　　　　  ·=

　 于是得到6s－9t+4=0　∵0<s<1, 0<t<1

　 ∴可取s=，t=

也就是说1转为0的概率为，0转为1的概率为.

注：第(3)问答案不惟一，只要满足方程6s－9t+4=0 (0<s<1, 0<t<1)的s，t均可。