高二数学下学期月考试卷
（范围：选修2-2）
姓名 班级 学号 得分
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）
1．复数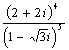
等于 A．
B．－ C．
D．－ （ ）
2．用数学归纳法证明凸 n 边形对角线为
时，第一步要验证n= （ ）
A．1 B．
3．设
则以下结论中正确的是 （ ）
A．z对应的点在第一象限； B．z一定不是纯虚数；C．z对应的点在实轴上方； D．z一定是实数；
4．设
是可导函数，且
，则
（ ）
A．
B．
C．
D．
5．函数
、直线
、直线
所围成的区域面积是 （ ）
A．
B．
C．
D．
6．若
且
，则
的最小值是 （ ）
A．
B．
C．
D．
7．已知函数的导数
,且图象过点（0,-5）,当函数取得极大值-5时,x的值应为 A．
B．
（ ）
8．已知
＝2，关于p＋q的取值范围的说法正确的是 （ ）
A．一定不大于2
B．一定不大于
C．一定不小于
D．一定不小于2
9．若
，0<a<b<e，则有 （ ）
A．
B．
C．
D．
10．在平面几何里，有射影定理：“设
的两边AB、AC相互垂直，AD是斜边BC上的高，则
”。拓展到空间，类比平面几何的射影定理，“在三棱锥
中，
，A在
内的射影为O”，则可得 （ ）
A．
B．
C．
D．
11．如果函数
的图象在
处的切线
过点（
），并且l与圆C：
相离，则点
与圆C的位置关系是 （ ）
A．在圆内 B．在圆外 C．在圆上 D．不能确定
12．在抛物线
上找一点P
，其中
，过点P作抛物线的切线，使此切线与抛物线及两坐标轴所围平面图形的面积最小 （ ）
A．
B．
C．
D．
二、填空题：请把答案填在题中横线上（每小题6分，共24分）
13．
.
14．在平面内，三角形的面积为s，周长为c，则它的内切圆的半径
.在空间中，三棱锥的体积为V，表面积为S，利用类比推理的方法，可得三棱锥的内切球（球面与三棱锥的各个面均相切）的半径R=
.
15．如图,它满足(1)第n行首尾两数均为n,(2)表中的递推关系类似杨辉三角,则第n行(n
2)第二个数是 _____
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5
6 16 25 25 16 6
16．有如下命题，
（1）已知
，且
则
（2）已知
对一切自然数n都成立，那么这样的实数a,b,c不存在； （3）否定结论“至多有两个解”，可以用“至少有两个解”；
（4）复数z是一个实数的充要条件是z=
，且z是一个虚数的充要条件是z+是一个实数；
（5）若
，则
；其中正确的命题有
三、解答题：解答应写出文字说明、证明过程或演算步骤（共76分）.
17．设关于
的方程
的两根的模的和为，求实数
的值.
18． 设
，（1）若在
处有极值，求a；
（2）若在
上为增函数，求a的取值范围.
19．已知
，其中
（1）证明：若
，则
（2）试问（1）的逆命题是否成立？若成立给予证明，若不成立说明理由或给出反例.
20．（12分）已知数列
为其前n项和，计算得
,
,观察上述结果，推测出计算Sn的公式，并用数学归纳法加以证明．
21．抛物线
在第一象限内与直线x+y=4相切,此抛物线与x轴围成的图形的面积为S.求使S达到最大值的a,b值,并求此最大值．
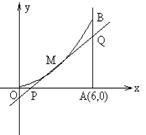22．（14分）如图所示，曲线段OMB是函数f(x)＝x2(0＜x＜6＝的图象，BA⊥x轴于A，曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P，交线段AB于Q，⑴试用t表示切线PQ的方程；⑵试用t表示出△QAP的面积g(t)；若函数g(t)在(m，n)上单调递减，试求出m的最小值；⑶若S△QAP∈[
]，试求出点P横坐标的取值范围