高二数学下学期期中考试试卷
高二数学(Ⅰ)
考生注意:1.请把选择题、填空题的答案写在第二卷对应栏中,第一卷不交。
2.满分150分.考试用时120分钟。
一．选择题 （本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的,请把正确答案的代号在答题卡中涂黑．）
1. 棱长为a的正方体ABCD-A1B
A.30° B.45° C.60° D.90°
2. 已知
，且
，则
A.1 B
3. 
平面α所成角的取值范围是
4. 设O、A、B、C是不共面的四点，对于空间一点P，使四点P、A、B、C共面的条件是
5. 已知平面
所成的二面角为80°，P为
、
外一定点，过点P的一条直线与
,所成的角都是30°，则这样的直线有且仅有
A.1条 B.2条 C.3条 D.4条
6. 下列命题中：①过一点一定存在和两条异面直线都平行的平面；②两条平行线中的一条与平面平行，则另一条也和这个平面平行；③一条直线平行于一个平面，则夹在它们之间的平行线段长相等；④平行于同一个平面的两条直线互相平行；其中正确的是
A.③ B.①②③ C.③④ D.②③④
7. 
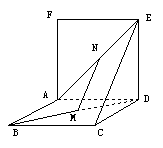如图所示，空间中有两个正方形ABCD和ADEF，设M、N分别是BD和AE的中点，那么①
；②
面
；③
； ④
、
是异面直线；以上四个命题中正确的个数是
A.1 B
8. 在正四面体ABCD中，E为AB中点，F为△BCD的中心，则EF与BC所成的角为.
A.30° B.45° C.60° D.90°
9. 正方形ABCD，沿对角线BD折成直二面角后不会成立的结论是
A.AC⊥BD B.△ADC为等边三角形
C.AB、CD所成角为60° D.AB与平面BCD所成角为60°
10. 用四种不同颜色给正方体ABCD—A1B
A.24种 B.72种 C.96种 D.48种
第Ⅱ卷（非选择题 共5道填空题6道解答题）
二.简答题 （本大题共5小题，每小题5分，共25分．把答案填在答题卡的横线上）
11. 锥体体积V可以由底面积S与高h求得：
. 已知正三棱锥P—ABC底面边长为2
，体积为4，则底面三角形ABC的中心O到侧面PAB的距离为 .
12. 用棱长为
的正方体形纸箱放一棱长为
的正四面体形零件，使其能完全放入纸箱内，则此纸箱容积的最小值为 。
13. (文)地球北纬45o圈上有A,B两地，点A在东经130o处，点B在西经140o处，若地球半径为R，则A、B两点在纬度圈上劣弧长与A、B两点的球面距离之比是_________
(理)若定义运算
，则符合条件
的复数
为 。
14. 从一点O出发的三条射线OA、OB、OC两两成60°角，则OA与平面OBC所成的角的大小为_______
15. 已知平面
和直线，给出条件：①
；②
；③
；④
；⑤
.（i）当满足条件
时，有
；（ii）当满足条件
时，有
.（填所选条件的序号）
高二数学(Ⅱ)
请把选择题中你认为正确答案代号在答题卡中涂黑
|
请把填空题的答案填在下面空中
11________________ 12._____________ 13.(文)__________(理)__________
14.________________ 15.______________
总分栏
| 一 | 二 | 16 | 17 | 18 | 19 | 20 | 21 | 总分 |
三.解答题 （本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．）
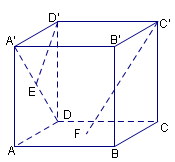16.（本小题满分12分）如图，在正方体
中，
是
的中点，
是正方形
的中心，求
与
的夹角。
17.（本小题满分12分）求证：如果一个平面与另一个平面的垂线平行，那么这两个平面互相垂直.
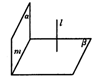已知：
求证：
证明：
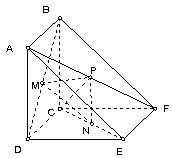18.（本小题满分12分）如图，已知正方形ABCD和正方形CDEF所在的平面相互垂直，且边长为a，M、N、P分别是BD、CE、AF的中点.
(1)判断四边形ABFE的形状并证明；
(2)求异面直线BD和CP所成的角；
(3)判断△MNP的形状并证明.
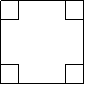
19.（本小题满分12分）有一块边长为4的正方形钢板，现对其进行切割、焊接成一个长方体无盖容器（切、焊损耗忽略不计），有人应用数学知识作了如下设计：如图（a），在钢板的四个角处各切去一个小正方形，剩余部分围成一个长方体，该长方体的高为小正方形边长，如图（b）,
(1)请你求出这种切割、焊接而成的长方体的最大容积V
；(文科只要求写出表达式,不用求最值,理科请注意公式
)
(2)由于上述设计存在缺陷（材料有所浪费），请你重新设计切焊方法，使材料浪费减少，而且所得长方体容器的容积V
>V
.
x
图（a） 图（b）
20.（本小题满分13分）在四棱锥PABCD中，底面ABCD是矩形，侧棱PA垂直于底面，E、F 分别是AB、PC的中点，
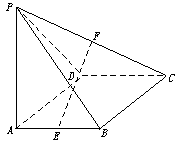(1)求证：CD⊥PD；
(2)求证：EF∥平面PAD；
(3)当平面PCD与平面ABCD成多大角时，直线EF⊥平面PCD.
21.（本小题满分14分）如图,异面直线AC与BD的公垂线段AB=4,又AC=2,BD=3,CD=4
.
⑴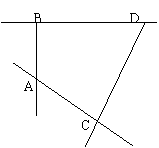
求二面角C—AB—D的大小；
⑵求点C到平面ABD的距离；
⑶求异面直线AB与CD间的距离。
武昌区07－08年度下学期期中考试
参考答案（仅供参考）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | C | B | D | D | A | C | C | D | C |
8. 取AC中点G，则EG∥BC且EG=
，则∠GEF为EF与BC所成角，连结BF，CF，则FE.FG分别为Rt△ABFRt△ACF的斜边上的中线，∴
，∴△EFG为正△，∴选C。
二.简答题答案:
11.
12.
13. (文)
︰4 (理) 
14. 
15. ③⑤ ； ②⑤
三.解答题答案:
16. 分别以DA,DC,DD’所在的直线为x,y,z轴建立右手坐标系，设正方体棱长为1，则
，
，
，
，夹角为
17. 已知：α∩β=m，l⊥β，l∥α.
求证：α⊥β.
证明：在α内任取一点P，
∵l∥α， ∴P
l.设l和点P确定的平面为γ.
设γ∩α=l′，则l∥l′
l⊥β 
l′⊥β
α⊥β.
l∥l′ l′
α
18. （1）由AB平行且等于CD，CD平行且等于EF，有AB平行且等于EF，从而四边形ABFE是平行四边形
∵ 平面AC⊥平面DF，AD⊥CD，∴AD⊥平面DF，AD⊥EF
又EF⊥DE，∴EF⊥平面ADE ∴EF⊥AE
∴平行四边形ABFE是矩形且不是正方形
（2）如图，建立空间直角坐标系，则C（0，0，0），D（a，0，0），
|
，，）,
则
=（a,0,-a），
=（,,）
∵
·=
+0-=0
∴⊥，即BD与CP所成的角是90°
（3）由P（，，），N（，，0），M（，0，），
得 
=（0，-，0），
=（0，0，-）
∵
·
=0， ∴⊥
又=,所以△MNP是等腰直角三角形.
另解提示:用非向量的方法解(2)与(3)时,可行先连结BE与DF,再进行推理与运算.
19. (1)设切去正方形边长为
，则焊接成的长方体的底面边长为
,高为
,所以
,
因为x(4-2x)(4-2x)=
4x(4-2x)(4-2x)≤
∴当且仅当=
时, 
取最大值
.
(2)重新设计方案如下：
如图①，在正方形的两个角处各切下一个边长为1的小正方形；如图②，将切下的小正方形焊在未切口的正方形一边的中间；如图③，将图②焊成长方体容器.
新焊长方体容器底面是一长方形，长为3，宽为2，此长方体容积
=3×2×1=6，显然>，故第二种方案符合要求.
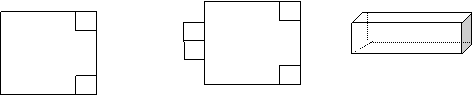3
1
1
4
3
图① 图② 图③
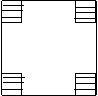
4
 |
图④ 图⑤
另外，还可以如图④
=2×4×=
> 还可以如图⑤
=
××
=
> .
20. (1)证明：∵ABCD是矩形∴CD⊥AD又∵PA⊥平面ABCD，
AD是PD 在平面ABCD上的射影,由三垂线定理：CD⊥PD
(2)证明：取CD中点N，连结EN、FN∵E、F分别是AB、PC的中点
∴FN∥PD,EN∥AD.∵FN
平面PAD，EN平面PAD∴FN∥平面PAD，
EN∥平面PAD,∵FN∩EN=N∴平面EFN∥平面PAD
∵ EF平面EFN，∴EF∥平面PAD
(3)当平面PCD与平面ABCD成45°角时，直线EF⊥平面PCD
∵AB∥CD∴CD⊥AD,PD⊥CD,即∠PDA就是侧面PCD与底面ABCD所成二面角的平面角.
连结PE，EC又∠PDA=45°∴PA=AD=BC,又AE=EB∴Rt△PAE≌Rt△CBE
∴PE=EC ,∵F为PC的中点∴EF⊥PC，又FN∥PD,EN∥AD∴CD⊥FN,∴CD⊥EN
∴CD⊥平面EFN∴CD⊥EF∵CD∩PC=C,∴EF⊥平面PCD
21. ⑴过A作AE∥BD，过D在作DE⊥AE，垂足为E，
AB⊥BD ∴AB⊥AE
又 AB⊥AC ∴∠CAE
为二面角C－AB－D的平面角，这时AB ⊥平面ACE，于是DE⊥ 平面ACE,连CE在Rt△CDE中，CD=4，DE=AB=4，∴CE=4，在△ACE中，AE=BD=3，AC=2，由余弦定理得
即二面角C—AB—D
的大小为
；
⑵由⑴可知
，过C在平面ACE内作CH⊥AE，垂足为H，∵AB⊥平面ACE，∴平面ABD⊥平面ACE，∴CH⊥平面ABD，则CH为C到平面ABD的距离， 
；
⑶∴AB∥DE，∴AB与平面CDE的距离即AB与CD的距离，在平面ACE内作AN⊥CE，垂足为N， DE⊥平面ACE。 ∴平面CDE⊥平面ACE，于是AN⊥平面CDE。则AN为AB与平面CDE的距离。在△ACE中可得AN=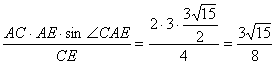
，即AB与CD的距离为
。