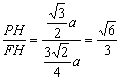高二数学下学期统考统阅试卷

高二数学下学期统考统阅试卷

一、选择题：

1、设=（　 ）

　　　 A．287　　　　　　　　　　 B．288　　　　　　　　　　 C．289　　　　　　　　　　 D．290

2、正方体的内切球与外接球的半径之比为　　　　　　　　　　　　　　　【　　　】

A、∶1　　　　　　　　　 B、∶2　　　　　 C、 1∶　　　　　　　　　D、2∶

3、若正四棱锥的全面积是底面积的3倍，则侧面与底面所成的角为　【　　　】

A、30°　　　　　　　　　　　B、45°　　　　　　　　　　　 C、 60°　　　　　　　　　　 D、75°

4、先后二次抛掷一枚均匀的硬币，其正反面各出现一次的概率为　　 【　　　】

A、　　　　　　　　　　　　　B、　　　　　　　　　　　　　C、　　　　　　　　　　　　　D、１

5、　  甲乙两气象站同时独立地对某地作气象预报，若甲气象站预报准确的概率为p，乙气象站预报不准确的概率为q，则在一次预报中，甲乙两气象站都预报准确的概率是　　【　　　】

A、pq　　　　　　　　　　　　　B、p(1-q)　　　　　　　　　　 C、q(1-p)　　　　　　　　　　D、(1-p)(1-q)

6、袋中有红、黄、白色球各一个，每次任取一个，有放回地抽取3次，则下列事件中概率为的是　

A、颜色全同　　　　　　　 B、颜色不全同　　　　　　C、 颜色全不同　　　　　 D、颜色无白色

7、3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士,不同的分配方法共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　【　　　】

A、90种　　　　　　　　　　　B、180种　　　　　　　　　　C、720种　　　　　　　　　　D、540种

8、某人射击的命中率为0.6，则他射击8枪中有5枪命中，且有且仅有4枪连在一起的概率为【 】

A、　　　 B、　C、D

9、如图，在斜三棱柱ABC－A₁B₁C₁中，∠BAC=90°，又BC₁⊥AC，过C₁作C₁H⊥底面ABC，垂足为H，则点H一定在　　【　　　】

A、直线AC上　　　B、直线AB上　 C、直线BC上　　　 D、△ABC的内部

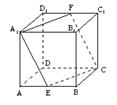10、正方体ABCD－A₁B₁C₁D₁中，E、F分别为棱AB、C₁D₁的中点，则A₁B₁与截面A₁ECF所成角的正弦值为　【　　　】

A、　　　　　　　　B、　　　　　　　　 C、　　　　　　　　D、

二、填空题：

11、已知的展开式中的系数为，常数a的值为__________．

12、8件产品中有2件次品，从中任取两件，则至少取到1件次品的概率是__________．

13、甲、乙、丙三人独立地破译一个密码，他们能译出的概率分别为、、，则该密码被破译的概率是__________．

14、长方体的长、宽、高之和为12，对角线长为8，则它的全面积为________．

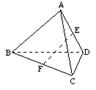
15、在三棱锥A－BCD中，平面ABD⊥平面BCD，∠BDC＝90°，E、F分别是AD、BC的中点，若EF＝CD，则EF与平面ABD所成的角为___________．

三、解答题：

16、6人到6个地方去旅游，每个人去一个地方，每个地方去一个人。

（1）甲去A地、乙去B地、丙去C地，共有多少种旅游方案？

（2）甲不去A地、乙不去B地、丙不去C地，共有多少种旅游方案？

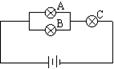17． 图中灯泡A，B，C是否正常是相互独立的，它们不亮的概率分别是0.1，0.2，0.1　．

（Ⅰ）求所有灯泡都亮的概率；

（Ⅱ）求有灯泡亮也有灯泡不亮的概率．

18、如图，正方体ABCD－A₁B₁C₁D₁中，E，Ｆ分别为AB与BB₁的中点，

（Ⅰ）求证：EF⊥平面A₁D₁B ；

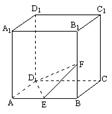（Ⅱ）求二面角F－DE－C大小的正切值．

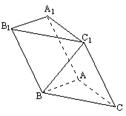
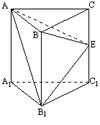19．如图，正三棱柱ABC一A₁B₁C₁的棱长均为2a，E为CC₁的中点．

（Ⅰ）求证：AB₁⊥BE ；

（Ⅱ）求三棱锥B一AB₁E的体积．

20.有9件电子产品，其中6件正品3件次品.

（1）如果一次取出3件测试，求至少抽到两件正品的概率；

（2）若不放回一个一个的测试，求六次测试恰好全部抽到正品的概率；

（3）若不放回一个一个的测试，求经过六次测试恰好将3个次品全部找出的概率.

21．已知在四棱锥P­一ABCD中,二面角P一AD一B为60°,

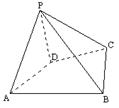∠PDA=45°,∠DAB=90°,∠PAD=90°,∠ADC=135°,

（Ⅰ）求证：平面PAB⊥平面ABCD；

（Ⅱ）求PD与平面ABCD所成角的正弦值；

（Ⅲ）求二面角P一CD一B的正切值．

【参考答案】

一、1、A　　　　2、C　　　　3、C　　　　4、C　　　　5、B

　　6、C　　　　7、D　　　　8、D　　　　9、B　　　　10、B

二、11、4　 12、　　　　 13、　　　14、80　　　15、30°

三、16、解：（1）=6种方案（5分）

（2）6个人赴6个地方共有种可能。

①若甲、乙、丙同时都去各自不能去的地方旅游，而其余的人去余下的地方旅游的有=6种；

②若甲、乙、丙中有2人同时去各自不能去的地方旅游有种，而3人中剩1人，是种，无条件3人的旅游方法是种，所以共有=54种。（9分）

③若甲、乙、丙中有1人去自己不能去的地方有种，而余下的5人共有种，有2人去自己不能去的地方和1人去自己不能去的地方，共有（--）种。

故满足条件的方案有-（6+54+234）=426（种）。（12分）　　　

17、解：（I）记事件A₁、A₂、A₃分别表示灯泡A、B、C不亮，它们相互独立，则所有灯泡都亮的概率为：

P()=P=(1-0.1)×(1-0.2)×(1-0.1)=0.648

(II)A、B中有一只亮，一只不亮，C必须亮，即求概率为

P

=0.1×(1-0.2)×(1-0.1)+(1-0.1)×0.2×(1-0.1)=0.234

18、证明：（I）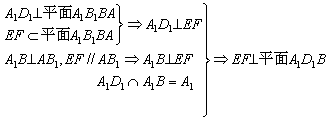

解：（II）延长DE、CB交于N，∵E为AB中点，∴△DAE≌△NBE

过B作BM⊥EN交于M，连FM，∵FB⊥平面ABCD

∴FM⊥DN，∴∠FMB为二面角F—DE—C的平面角

设AB=a，则BM=　　又BF=

∴tan∠FMB=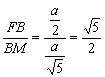，即二面角F—DE—C大小的正切值为

19、证明：（I）取BC中点M，连AM，B₁M，则AM⊥BC，

∵BB₁⊥平面ABC，∴BB₁⊥AM，BC∩BB₁=B

∴AM⊥平面BB₁C₁C 

由条件△BCE≌△B₁BM，∴∠BB₁M=∠CBE，而∠CBE+∠EBB₁=90°

∴∠BB₁M+∠EBB₁=90°，则B₁M⊥BE

∵B₁M为B₁A在平面BB₁C₁C上的射影，∴AB₁⊥BE

（II）

20、　　　　　　

21、、证明：（I）

（II）∵平面PAB⊥平面ABCD，过P作PH⊥AB交于H，则PH⊥平面ABCD

　　　　连DH，则∠PDH为PD为平面ABCD所成角

　　　∵DA⊥AB，DA⊥PA，∴∠PAB为二面角P—AD—B的平面角，∠PAB=60°

　　　设PA=a，则AD=a，PD=a，PH=a，∴sin∠PDH=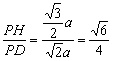

　　　则PD与平面ABCD所成角的正弦值为

（III）延长CD、BA交于E，过H作HF⊥CE于F，连PF，∵PH⊥平面ABCD，∴PF⊥CE

　　　∴∠PFH为二面角P—CD—B的平面角

　　　∵∠ADC=135°，∴∠EDA=45°，则EA=AD=a，EH=，∵∠E=45°

　　　∴FH=EH·sin45°=，tan∠PFH=