高二数学下第二次月考试卷
 (理科)
(理科)
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷共4页,包含填空题(共14题)、解答题(共6题),满分160分,考试时间为120分钟。
2.答题前,请您务必将自己的姓名、考试证号用书写黑色字迹的
3.请认真核对答题纸密封线内规定填写的项目是否准确。
4.作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置,在其他位置作答一律无效.如有作图需要,可用2B铅笔作答,并请加黑加粗,描写清楚。
A.必做题部分
参考公式:![]()
参考数据
| P( | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一、填空题:本大题共14题,每小题5分,共70分,请将正确答案填写在答题纸的相应位置.
1.若 ![]() ,
, ![]() ,且
,且![]() 为纯虚数,则实数
为纯虚数,则实数![]() 的值为 ▲ .
的值为 ▲ .
2.![]() 展开式中的
展开式中的![]() 系数为 ▲ .(用数字作答)
系数为 ▲ .(用数字作答)
3.在用反证法证明“圆内不是直径的两弦,不能互相平分”,假设 ▲ .
4.从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有 ▲ .
5.设A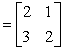 ,X
,X![]() , B
, B![]() ,满足AX=B,则
,满足AX=B,则![]() = ▲ .
= ▲ .
6.如果![]() ~
~![]() ,则当
,则当![]() 取得最大值时
取得最大值时![]() 的值为 ▲ .
的值为 ▲ .
7.![]() = ▲ .
= ▲ .
8.已知抛物线的极坐标方程是![]() ,则此抛物线的准线的极坐标方程是
,则此抛物线的准线的极坐标方程是
▲ .
9.一个均匀的小正方体的六个面中,三个面上标以数0,两个面上标以1,一个面上标以2,将这个小正方体抛掷两次,则向上的数之积的数学期望是 ▲ .
10.设![]() ,则
,则![]() ▲
.
▲
.
11.给出下列命题:①若![]() ,则
,则![]() 是纯虚数;②复数
是纯虚数;②复数![]() 的几何意义是将向量
的几何意义是将向量![]() 绕原点O逆时针旋转90°;③若
绕原点O逆时针旋转90°;③若![]() 是纯虚数,则实数
是纯虚数,则实数![]() =±1;④若
=±1;④若![]() =1,则复数z 一定等于1.其中,正确命题的序号是
▲ .
=1,则复数z 一定等于1.其中,正确命题的序号是
▲ .
12.已知函数![]() 满足:
满足:![]() ,
,![]() ,则有:
,则有:
![]() ▲
.
▲
.
13.若![]() 中两直角边为
中两直角边为![]() ,斜边
,斜边![]() 上的高为
上的高为![]() ,则
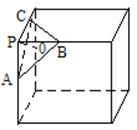
,则![]() ;如图,在正方体的一角上截取三棱锥
;如图,在正方体的一角上截取三棱锥![]() ,
,![]() 为棱锥的高,记
为棱锥的高,记![]() ,
,![]() ,那么
,那么![]() 的大小关系是 ▲ .
的大小关系是 ▲ .
14.已知![]() ,把数列
,把数列![]() 的各项排成右图所示的三角形的形状,记
的各项排成右图所示的三角形的形状,记![]() 表示第
表示第![]() 行,第
行,第![]() 列的项, 则
列的项, 则![]() ▲ .
▲ .
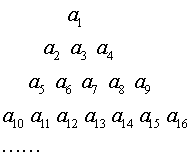
(第13题) (第14题)
二、解答题:本大题共6小题;共90分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
设m,n∈N,m、n≥1,f(x)=(1+x)m+(1+x)n的展开式中,x的系数为19.
(1)求f(x)展开式中x2的系数的最大、小值;
(2)对于使f(x)中x2的系数取最小值时的m、n的值,求x7的系数。
16.(本小题满分14分)
某高校调查询问了56名男女大学生,在课余时间是否参加运动,得到下表所示的数据。从表中数据分析,有多大把握认为大学生的性别与参加运动之间有关系。
| 参加运动 | 不参加运动 | 合计 | |
| 男大学生 | 20 | 8 | 28 |
| 女大学生 | 12 | 16 | 28 |
| 合计 | 32 | 24 | 56 |
17.(本小题满分14分)
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内.
(1)只有一个盒子空着,共有多少种投放方法?
(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
18.(本小题满分16分)
是否存在实数a、b使等式![]() 对任意的正整数n都成立,若不存在,说明理由;若存在,试确定a、b的值,并用数学归纳法证明之。
对任意的正整数n都成立,若不存在,说明理由;若存在,试确定a、b的值,并用数学归纳法证明之。
19.(本小题满分16分)
在一个盒子中,放有标号分别为![]() ,
,![]() ,
,![]() 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为![]() 、
、![]() ,记
,记![]() .
.
(Ⅰ)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
20.(本小题满分16分)
已知关于![]() 方程
方程![]() 有实根
有实根![]() ,
,
(1)求实数![]() 的值;
的值;
(2)若复数![]() 满足
满足![]() 求
求![]() 为何值时,
为何值时,![]() 有最小值并求出最小值。
有最小值并求出最小值。
B.附加题部分
(满分40分,考试时间30分钟)
本大题共4小题,每小题10分,共40分.解答时应写出文字说明、证明过程或演算步骤.
1.从4名男生和2名女生中任选3人参加演讲比赛,设随机变量![]() 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(Ⅰ)求![]() 的分布列;
(Ⅱ)求
的分布列;
(Ⅱ)求![]() 的数学期望;
的数学期望;
(Ⅲ)求“所选3人中女生人数![]() ”的概率.
”的概率.
2.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() ,
,![]() 相交于
相交于![]() ,
,![]() 两点. (Ⅰ)把曲线
两点. (Ⅰ)把曲线![]() ,
,![]() 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(Ⅱ)求弦![]() 的长度.
的长度.
3.(1)请说明下列矩阵A、B表示的几何意义,并求出矩阵AB的逆矩阵;
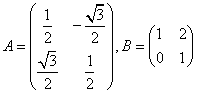
(2)设![]() ,若矩阵
,若矩阵![]() 把直线l:x+y-1=0变为直线m:x-y-2=0,求
把直线l:x+y-1=0变为直线m:x-y-2=0,求![]()
4.给定矩阵A=![]() ,B=
,B=![]() .
(1)求A的特征值λ1,λ2及对应特征向量α1,α2;
(2)求A4B.
.
(1)求A的特征值λ1,λ2及对应特征向量α1,α2;
(2)求A4B.

答案纸 (必做题部分)
高二数学(理科)
一.填空题:(本大题共14小题,每小题![]() 分,共70分.请把结果直接填在题中横线上)
分,共70分.请把结果直接填在题中横线上)
1. __________________ 2. ___________________________
3. __________________ 4. ___________________________
5. __________________ 6. ___________________________
7. __________________ 8. ___________________________
9. __________________ 10. __________________________
11. _________________ 12. __________________________
13. _________________ 14. __________________________
二.解答题:(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)
15.
16.
17.
18.
 19.
19.
20.

答案纸 (附加题部分)
本大题共4小题,每小题10分,共40分.解答时应写出文字说明、证明过程或演算步骤.
1.
2.
3.
4.
高二数学
参考答案及评分标准
A.必做题部分
参考公式:![]()
参考数据
| P( | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一、填空题:本大题共14题,每小题5分,共70分,请将正确答案填写在答题纸的相应位置.
1.若 ![]() ,
, ![]() ,且
,且![]() 为纯虚数,则实数
为纯虚数,则实数![]() 的值为
的值为 ![]() .
.
2. ![]() 展开式中的
展开式中的![]() 系数为 -960 .(用数字作答)
系数为 -960 .(用数字作答)
3. .在用反证法证明“圆内不是直径的两弦,不能互相平分”,假设 圆内不是直径的两弦,能互相平分.
4.从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有60 .
5.设A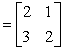 ,X
,X![]() , B
, B![]() ,满足AX=B,则
,满足AX=B,则![]() =
= ![]() .
.
6.如果![]() ~
~![]() ,则当
,则当![]() 取得最大值时
取得最大值时![]() 的值为
的值为 ![]() .
.
7.![]() =
= ![]() .
.
8.已知抛物线的极坐标方程是![]() ,则此抛物线的准线的极坐标方程是
,则此抛物线的准线的极坐标方程是
![]() cosθ=-
cosθ=-![]() .
.
9.一个均匀的小正方体的六个面中,三个面上标以数0,两个面上标以1,一个面上标以2,将这个小正方体抛掷两次,则向上的数之积的数学期望是 ![]() .
.
10.设![]() ,
,
则![]()
![]() .
.
11.给出下列命题:①若![]() ,则
,则![]() 是纯虚数;②复数
是纯虚数;②复数![]() 的几何意义是将向量
的几何意义是将向量![]() 绕原点O逆时针旋转90°;③若
绕原点O逆时针旋转90°;③若![]() 是纯虚数,则实数
是纯虚数,则实数![]() =±1;④若
=±1;④若![]() =1,则复数z 一定等于1.其中,正确命题的序号是
② .
=1,则复数z 一定等于1.其中,正确命题的序号是
② .
12.已知函数![]() 满足:
满足:![]() ,
,![]() ,则有:
,则有:
![]() 24 .
24 .
13.若![]() 中两直角边为
中两直角边为![]() ,斜边
,斜边![]() 上的高为
上的高为![]() ,则
,则![]() ;如图,在正方体的一角上截取三棱锥
;如图,在正方体的一角上截取三棱锥![]() ,
,![]() 为棱锥的高,记,
为棱锥的高,记, ![]() ,
,![]() ,那么
,那么![]() 的大小关系是
的大小关系是 ![]()
14. 已知![]() ,把数列
,把数列![]() 的各项排成右图所示的三角形的形状,记
的各项排成右图所示的三角形的形状,记![]() 表示第
表示第![]() 行,第
行,第![]() 列的项, 则
列的项, 则![]()
![]() .
.

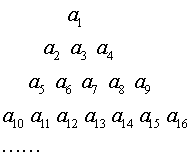
(第13题) (第14题)
二、解答题:本大题共6小题;共90分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
设m,n∈N,m、n≥1,f(x)=(1+x)m+(1+x)n的展开式中,x的系数为19.
(1)求f(x)展开式中x2的系数的最大、小值;
(2)对于使f(x)中x2的系数取最小值时的m、n的值,求x7的系数。
解:![]() 。
。![]()
(1)设x2的系数为T=![]()
![]() 。
。
∵n∈Z+,n≥1,∴当![]() 当
当![]() 。
。
(2)对于使f(x)中x2的系数取最小值时的m、n的值,即![]()
从而x7的系数为![]() 。
。
16.(本小题满分14分)
某高校调查询问了56名男女大学生,在课余时间是否参加运动,得到下表所示的数据。从表中数据分析,有多大把握认为大学生的性别与参加运动之间有关系。
| 参加运动 | 不参加运动 | 合计 | |
| 男大学生 | 20 | 8 | 28 |
| 女大学生 | 12 | 16 | 28 |
| 合计 | 32 | 24 | 56 |
解:设性别与参加体育运动无关
∵![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴![]() 的观测值为
的观测值为![]() ----8分
----8分
∵![]() ―――-------10分
―――-------10分
故有95%把握认为性别与参加运动有关。 ---------14分
17.(本小题满分14分)
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内.
(1)只有一个盒子空着,共有多少种投放方法?
(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
解:(1)C
(2)A55-1=119(种)
(3)满足的情形:第一类,五个球的编号与盒子编号全同的放法:1种
第二类,四个球的编号与盒子编号相同的放法:0种
第三类,三个球的编号与盒子编号相同的放法:10种
第四类,二个球的编号与盒子编号相同的放法:
∴ 满足条件的放法数为: 1+10+20=31(种)
18、(本小题满分16分)
是否存在实数a、b使等式![]() 对任意的正整数n都成立,若不存在,说明理由;若存在,试确定a、b的值,并用数学归纳法证明之。
对任意的正整数n都成立,若不存在,说明理由;若存在,试确定a、b的值,并用数学归纳法证明之。
解:存在
当n=1时22=1×2×(a+b) 得a+b=2
当n=2时22+42=2×3(
所以得![]() …….5分
…….5分
证明:(1)当n=1时,由以上知等式成立………………………………6分
(2)假设当n=k时等式成立,即
![]()
则![]() ……8分
……8分
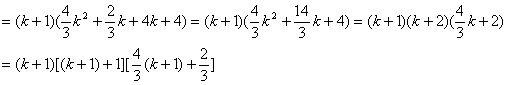
所以当n=k+1时等式也成立……………………………………………………14分
由(1)(2)知对于任意正整数n等式
![]() 都成立…………………… 16分
都成立…………………… 16分
19.(本小题满分16分)
在一个盒子中,放有标号分别为![]() ,
,![]() ,
,![]() 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为![]() 、
、![]() ,记
,记![]() .
.
(Ⅰ)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
解:(Ⅰ)![]() 、
、![]() 可能的取值为
可能的取值为![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
, ![]() ,且当
,且当![]() 或
或![]() 时,
时,![]()
因此,随机变量![]() 的最大值为
的最大值为![]() .
. ![]() 有放回抽两张卡片的所有情况有
有放回抽两张卡片的所有情况有![]() 种,
种,
![]() .答:随机变量
.答:随机变量![]() 的最大值为3,事件“
的最大值为3,事件“![]() 取得最大值”的概率为
取得最大值”的概率为![]() .
.
(Ⅱ)![]() 的所有取值为
的所有取值为![]() .
.
![]() 时,只有
时,只有![]() 这一种情况,
这一种情况,
![]() 时,有
时,有![]() 或
或![]() 或
或![]() 或
或![]() 四种情况,
四种情况,
![]() 时,有
时,有![]() 或
或![]() 两种情况.
两种情况.
![]() ,
,![]() ,
,![]() .
.
则随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
因此,数学期望![]() .
.
20.(本小题满分16分)
已知关于![]() 方程
方程![]() 有实根
有实根![]() ,
,
(1)求实数![]() 的值;
的值;
(2)若复数![]() 满足
满足![]() 求
求![]() 为何值时,
为何值时,![]() 有最小值并求出最小值。
有最小值并求出最小值。
.解:(1)∵ 关于![]() 方程
方程![]() 有实根
有实根![]() ,
,
∴ ![]() ,即
,即![]()
∴ ![]() ,解得:
,解得:![]()
(2)设![]()
![]() 、
、![]() ,代入
,代入![]() 得:
得:
![]() ∴
∴ ![]()
化简,整理得:![]()
∴ 复数z对应的点的轨迹是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,![]()
∴ ![]() ,由
,由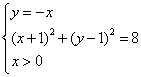 解得:
解得:![]()
∴ 当![]() 时,
时,![]() .
.
B.附加题部分
(满分40分,考试时间30分钟)
本大题共4小题,每小题10分,共40分.解答时应写出文字说明、证明过程或演算步骤.
1.从4名男生和2名女生中任选3人参加演讲比赛,设随机变量![]() 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)求![]() 的数学期望;
的数学期望;
(Ⅲ)求“所选3人中女生人数![]() ”的概率.
”的概率.
解:(Ⅰ)![]() 可能取的值为0,1,2.
可能取的值为0,1,2.
由题意:![]() ,
,
![]() .
.
所以,![]() 的分布列为:
的分布列为:
|
| 0 | 1 | 2 |
| P |
|
|
|
(Ⅱ)解:由(Ⅰ),![]() 的数学期望为
的数学期望为![]() .
.
(Ⅲ)解:由(Ⅰ),“所选3人中女生人数![]() ”的概率为
”的概率为
![]() .
.
2.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() ,
,![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(Ⅰ)把曲线![]() ,
,![]() 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(Ⅱ)求弦![]() 的长度.
的长度.
解:(Ⅰ)曲线![]() :
:![]() (
(![]() )表示直线
)表示直线![]() .曲线
.曲线![]() :
:![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
(Ⅱ)圆心(3,0)到直线的距离 ![]() ,
,![]() ,所以弦长
,所以弦长![]() =
=![]() .
.
3.(1)请说明下列矩阵A、B表示的几何意义,并求出矩阵AB的逆矩阵;
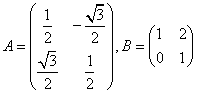
(2)设![]() ,若矩阵
,若矩阵![]() 把直线l:x+y-1=0变为直线m:x-y-2=0,求
把直线l:x+y-1=0变为直线m:x-y-2=0,求![]()
解:(1)A矩阵的几何意义:绕原点逆时针旋转600;
B矩阵的几何意义:纵坐标不变,横坐标增加纵坐标的2倍的切变变换
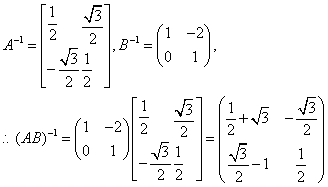
(2)法1、在l上任取一点P(x,y)经矩阵变换后为点![]() ,
,
则![]()
![]()
法2、在l上任取两点(1,0)与(0,1)
![]()
4.给定矩阵A=![]() ,B=
,B=![]() .
.
(1)求A的特征值λ1,λ2及对应特征向量α1,α2;
(2)求A4B.
解:(1)设A的一个特征值为λ,由题知![]() =0
=0
(λ-2)(λ-3)=0 λ1=2,λ2=3
当λ1=2时,由![]()
![]() =2
=2![]() ,得
A的属于特征值2的特征向量α1=
,得
A的属于特征值2的特征向量α1=![]()
当λ1=3时,由![]()
![]() =3
=3![]() ,得
A的属于特征值3的特征向量α2=
,得
A的属于特征值3的特征向量α2=![]()
(2)由于B=![]() =2
=2![]() +
+![]() =2α1+α2
=2α1+α2
故A4B=A4(2α1+α2)
=2(24α1)+(34α2)
=32α1+81α2
=![]() +
+![]()
=![]()