导数及其应用、推理证明练习
一、选择题
1.函数![]() 有( )
有( )
A.极大值![]() ,极小值
,极小值![]() B.极大值
B.极大值![]() ,极小值
,极小值![]()
C.极大值![]() ,无极小值
D.极小值
,无极小值
D.极小值![]() ,无极大值
,无极大值
2.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.曲线![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,则
,则![]() 点的坐标为( )
点的坐标为( )
A.![]() B.
B.![]() C.
C.![]() 和
和![]() D.
D.![]() 和
和![]()
4.![]() 与
与![]() 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若![]() ,
,![]() 满足
满足![]() ,则
,则![]() 与
与![]() 满足( )
满足( )
A.![]()
![]() B.
B.![]()
![]() 为常数函数
为常数函数
C.![]()
![]() D.
D.![]()
![]() 为常数函数
为常数函数
5.函数![]() 单调递增区间是( )
单调递增区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 设函数![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C. ![]() 中较小的数 D.
中较小的数 D. ![]() 中较大的数
中较大的数
8. 函数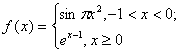 ,若
,若![]() 则
则![]() 的所有可能值为( )
的所有可能值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.函数![]() 在区间
在区间![]() 上的最大值是 。
上的最大值是 。
2.函数![]() 的图像在
的图像在![]() 处的切线在x轴上的截距为________________。
处的切线在x轴上的截距为________________。
3.函数![]() 的单调增区间为
,单调减区间为___________________。
的单调增区间为
,单调减区间为___________________。
4.若![]() 在
在![]() 增函数,则
增函数,则![]() 的关系式为是
。
的关系式为是
。
5.函数![]() 在
在![]() 时有极值
时有极值![]() ,那么
,那么![]() 的值分别为_________、_______。
的值分别为_________、_______。
6. (1)![]()
![]()
通过观察上述两等式的规律,请写出一般性的命题___________________________________
(2)![]()
![]()
通过观察上述两等式的规律,请你写出一般性的命题_________________________________
三、解答题
1.
已知曲线![]() 与
与![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值。
的值。
2. 若数列![]() 的通项公式
的通项公式![]() ,记
,记![]() ,试通过计算
,试通过计算![]() 的值,推测出
的值,推测出![]()
3. 已知![]() 的图象经过点
的图象经过点![]() ,且在
,且在![]() 处的切线方程是
处的切线方程是![]()
(1)求![]() 的解析式; (2)求
的解析式; (2)求![]() 的单调递增区间。
的单调递增区间。
4.平面向量![]() ,若存在不同时为
,若存在不同时为![]() 的实数
的实数![]() 和
和![]() ,使
,使![]()
![]() 且
且![]() ,试确定函数
,试确定函数![]() 的单调区间。
的单调区间。
5. ![]() 的三个内角
的三个内角![]() 成等差数列,求证:
成等差数列,求证:![]()
6.已知![]() 均为实数,且
均为实数,且![]() ,
,
求证:![]() 中至少有一个大于
中至少有一个大于![]() 。
。
一、选择题
1.C
2.D
![]()
3.C 4.B ![]() ,
,![]() 的常数项可以任意 5.C
的常数项可以任意 5.C
6.A 令![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,在定义域内只有一个极值,所以
,在定义域内只有一个极值,所以![]()
7.D
8..C ![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
二、填空题
1.![]()
![]() ,比较
,比较![]() 处的函数值,得
处的函数值,得![]()
2.![]()
![]()
3.![]()
![]()
![]()
4.![]()
![]() 恒成立,
恒成立,
则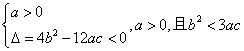
5.![]()
![]()
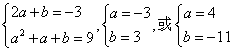 ,当
,当![]() 时,
时,![]() 不是极值点
不是极值点
6. (1) 若![]() 都不是
都不是![]() ,且
,且![]() ,则
,则![]()
(2) ![]()
三、解答题
1.解:![]()
![]() 。
。
2. ![]()
![]()
![]()
![]()
3.解:(1)![]() 的图象经过点
的图象经过点![]() ,则
,则![]() ,
,
![]()
切点为![]() ,则
,则![]() 的图象经过点
的图象经过点![]()
得![]()
![]()
(2)![]()
单调递增区间为![]()
4.解:由![]() 得
得![]()
![]()
![]()
![]()
![]()
所以增区间为![]() ;减区间为
;减区间为![]() 。
。
5.证明:要证原式,只要证![]()
即只要证![]() 而
而![]()
![]()
6.证明:假设![]() 都不大于
都不大于![]() ,即
,即![]() ,得
,得![]() ,
,
而![]() ,
,
即![]() ,与
,与![]() 矛盾,
矛盾, ![]() 中至少有一个大于
中至少有一个大于![]() 。
。