高二数学排列与组合单元测试

高二数学排列与组合单元测试(二)

命题人：沈红刚

　　　　班　　姓　　名　　　　　　　　　　　 　 学号　　　　 

一、选择题（本大题共12个小题；每小题3分，共36分．在每小题给出的四个选项中，只有一个符合题目要求，请将正确选项的代号填入答题卡的相应位置．）

1. 已知的二项展开式的第7项为，则x的值等于（　　）

A．　　　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　 D．

2 (普通班)若n为正奇数，则被9除所得余数是（　　 ）

A、0　　　　　　 B、3　　　　　　 C、－2　　　　　D、8

 (重点班)…除以88的余数是　 （　　）

A． －87　　　　　B． 1　　　　　  C．1　　　　　　　 D．87

3、如果的展开式中含有非零常数，则正整数n的最小值为（　　 ）

A、3　　　　　　 B、5　　　　　　 C、6　　　　　　 D、10

4．已知，若

= 29－n，那么自然数n的值为（　　 ）

A．3　　　　  　 B．4 　　　　　 C．5　　　　　　   D．6

5．某城市的汽车牌照号码由2个英文字母后接4个数字组成，其中4个数字互不相同的牌照号码共有（　　）

Ａ．个 　Ｂ．个　 　　Ｃ．个　　　  Ｄ．个

6、设有编号为的四个球和编号为的四个盒子，现将这四个球投放到四个盒子内，恰有两个盒子不放球的不同放法种数为（　　 ）

A. 60　　　　  B. 72　　　　  C. 84　　　　 D. 120

7．的展开式中的系数为 （　　）

A．　　　　　　 B．　　　　　　　　 C．　　　　　　  D．

8．把9个相同的小球放入其编号为1，2，3的三个盒子里，要求每个盒子放球的个数不小于其编号数，则不同的放球方法共有(　　　 )

A．8种　　　 B．10种　　　　  C．12种　　　 D．16种

9、设的展开式中的各项系数之和为P，而它的二项式系数之和为S。若P+S=272，那么展开式中项的系数是：　　　　　　　　　　　　　　　　　　　　　　

A．81　　　　　　　　　　　 B．54　　　 　　 C．—12　　　　　　　 D．1

10、已知，从到的映射满足：

①；②中的元素在下不同的象有且只有3个，则适合条件的映射的个数是（　　　）

A．6　　　　　　　　　　　　　 B．10　　　　　　　　　　　　　C．60　　　　　　　　　　　　D．360

11.若展开式中各项系数之和为,则展开式中含的项是(　 )

（A）第3项　　　　　　　　　（B）第4项　　　　　 （C）第5项　　　　　 （D）第6项

12．若的展开式中，项的系数为36，则＝　　　　　　　　　  （　　）A．3　　 B． 　　　　　　　　　　　　　　　　　　　 C．3或　　　　　　D．2或

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二．填空题（本大题5小题，每小题4分，共20分）

13. 已知函数，R，则_____。

14 (重点班)．10张参观公园的门票分给5个班，有________种选法。

14(普通班).从1、2、3、4、…  、15这15个正整数中取出5个互不相邻的正整数, 则取法种数共有　　　　　　   .

15、在(1+x)⁵+(1+x)⁶+(1+x)⁷的展开式中，含x⁴项的系数是通项公式为a_n=3n-5的数列的第_____项。

16.求和：m!+++…+=__________.

17．从装有个球（其中个白球，1个黑球）的口袋中取出个球,共有种取法。在这种取法中，可以分成两类：一类是取出的个球全部为白球，一类是取出的个白球和1个黑球，共有，即有等式：成立。试根据上述思想化简下列式子：　　　　　　 。。

三．解答题: 本大题共5个小题，共44分，解答应写出文字说明、证明过程或演算步骤.

18　个排成一排，在下列情况下，各有多少种不同排法？

（1）甲排头，（2）甲不排头，也不排尾，（3）甲、乙、丙三人必须在一起，（4）甲不排头，乙不排当中（5）甲、乙、丙三人两两不相邻，（6）甲、乙之间有且只有两人。

19．在二项式的展开式中，前三项系数的绝对值成等差数列．

求展开式的第四项；　　

求展开式的常数项；

求展开式中各项的系数和。

20．（本小题满分8分）已知 展开式中的倒数第三项的系数为45，

求：⑴含的项；⑵系数最大的项．

21．在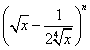的展开式中，前三项系数的绝对值成等差数列，

(1)　　求展开式中二项式系数最大的项；　　

(2)　　展开式中是否含有常数项？若有，请求出来；若没有，说明理由．

22．已知数列{a _n}是首项为a、公比为q的等比数列，

(1) 化简  以及 ；

（2）根据①的结果概括出关于正整数n的一个结论，并加以证明．

13.2

14．(重点班)解：10个空位加4个挡板位，共有14个放挡板的位置，有种方法。

15。理科20

14(普通班).

15．的展开式中常数项是____．（用数字作答）. 13．

16．解 ∵ ＝m!C_m+k^k

∴　原式＝m!(C_m+1⁰+C_m+1¹+C_m+2²+…+C_m+nⁿ)

＝m!C_m+n+1ⁿ＝

17.

18. 解：（1）甲固定不动，其余有，即共有种；

（2）甲有中间个位置供选择，有，其余有，即共有种；

（3）先排甲、乙、丙三人，有，再把该三人当成一个整体，再加上另四人，相当于人的全排列，即，则共有种；

（4）不考虑限制条件有，而甲排头有，乙排当中有，这样重复了甲排头，乙排当中一次，即

（5）先排甲、乙、丙之外的四人，有，四人形成五个空位，甲、乙、丙三人排

这五个空位，有，则共有种；

（6）从甲、乙之外的人中选个人排甲、乙之间，有，甲、乙可以交换有，

把该四人当成一个整体，再加上另三人，相当于人的全排列，

则共有种；

19．解:展开式的通项为，r=0，1，2，…，n

 由已知：成等差数列　　∴

∴ n=8　　　　　　　　　　　　　　　　　  ……4分

　 （1）　　　　　　　　　　　　　　 ……6分

　 （2）　　　　　　　　　　　　　　　 ……8分

（3）令x=1，各项系数和为　　　　　　 ……10分

20．⑴由题设知

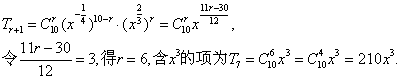
 ⑵系数最大的项为中间项，即

21．解：

　　　　　  n=8　　　　　　　　　　　　　　　　　　　　　　　　　 4ˊ

(1) 展开式中二项式系数最大的项

　　 T₅ = =　　　　　　　　　　　　　　　 4ˊ

(2)　T_r+1 = 　　　　　　　　　　　　　　　　　　　 3ˊ

　　由=0　　 得 r=

　　而r= 不为正整数，所以不含有常数项。　　　　　　　　　  3ˊ

22．解：(1) = a(1–q)²  3ˊ

　　　　= a(1–q)³  3ˊ

(2)　=  ， 证明如下：　　　 4ˊ

　　左边 =

　　　　 =

　　　　= = 右边　　　　　　　　　　　　　　　　　　　　 4ˊ