泪水为你换来同情，汗水为你赢得成功，与其流泪，不如流汗
高二数学排列与组合单元测试(一)
命题人：沈红刚
一、选择题（本大题共12个小题；每小题3分，共36分．在每小题给出的四个选项中，只有一个符合题目要求，请将正确选项的代号填入答题卡的相应位置．）
1．用数字1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有（ ）
A.96个 B.24个 C.32个 D.36个
2．从1,3,5,7,9中任取3个数字, 从2,4,6,8中任取2个数字, 一共可以组成无重复数字的五位数的个数是 ( )
A． 
B．
C． 
D．
3．某人制定了一项旅游计划，从7个旅游城市中选择5个进行游览。如果A、B为必选城市，并且在游览过程中必须按先A后B的次序经过A、B两城市（A、B两城市可以不相邻），则有不同的游览线路 （ ）
A．120种 B．240种 C．480种 D．600种
4．从编号分别为：
的共
个球中，取出
只球，使只球的编号之和为奇数，其方法总数为 ………………………………（ ）
A、200 B、
5、4名医生分配到3个医疗队，每队至少去1名，则不同的分配方案有 …………（ ）
A、36种 B、72种 C、108种 D、144种
6、设集合A={1，2，3，4}，m、n∈A，则方程
表示焦点位于x轴上的椭圆有
A、6个 B、8个 C、12个 D、16个
7．将编号为1，2，3，4，5的五个球放入编号为1，2，3，4，5的五个盒子，每个盒内放一个球，若恰好有三个球的编号与盒子编号相同，则不同的投放方法的种数为:
A. 6种 B. 10种 C. 20种 D. 30种
8．北京《财富》全球论坛期间，某高校有14名志愿者参加接待工作．若每天排早、中、晚三班，每班4人，每人每天最多值一班，则开幕式当天不同的排班种数为（ ）
A．
B．
C．
D．
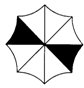9．如图，某伞厂生产的“太阳”牌太阳伞的伞蓬是由太阳光的七种颜色组成，七种颜色分别涂在伞蓬的八个区域内，且恰有一种颜色涂在相对区域内，则不同的颜色图案的此类太阳伞至多有
（ ）
A． 40320种 B． 5040种 C． 20160种 D． 2520种
10．将4个不同的小球放入甲、乙两个盒子中，每盒至少放一个小球，现有不同的放置方法，甲列式子：
；乙列式子：
；丙列式子：
；丁列式子：
，其中列式正确的是
A．甲 B．乙 C．丙 D．丁
11、若集合
，集合
，
是从
到
的映射，则满足
的映射有………………………………（ ）
A、6个 B、7个 C、8个 D、9个
12．某班团支部换届进行差额选举，从已产生的甲、乙、丙、丁四名候选人中选出三人分别担任书记、副书记和组织委员，并且规定：上届任职的甲、乙、丙三人不能连任原职，则不同的任职结果有（ ）
A．15种 B．11种 C．14种 D．23种
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二．填空题（本大题4小题，每小题3分，共12分）
13
在△
的边
上有个点，边
上有
个点，加上
点共12个点，以这
个点为顶点的三角形有 个
14、设含有5个元素的集合的全部子集数为
，其中由2个元素组成的子集的个数是
，
则
的值为_______________。
15. 若把英语单词“hello”的字母顺序写错了，则可能出现的错误有_______种.
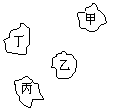
16、如图甲、乙、丙、丁为海上的四个小岛，要建三座桥，将这四个岛
连接起来，不同的建桥方案共有______________种（用数字作答）
三.解答题：本大题共6小题，共52分．解答应写出文字说明，证明过程或演算步骤．
17.(本小题满分8分）一个口袋内装有大小相同且编有不同号码的5个白球和4个黑球.
（1）从口袋内取出3个球，共有多少种取法？
（2）从口袋内取出3个球，使其中恰有1个黑球，共有多少种取法？
（3）从口袋内取出3个球，使其中至少有1个黑球，共有多少种取法？
18. (本小题满分8分) 用0，1，2，3，4，5这六个数字.（1）可以组成多少个无重复数字的三位数？（2）可以组成多少个无重复数字的三位奇数？（3）可以组成多少个大于3012且无重复数字的四位数？
19．（本小题满分9分）8名同学排成一排照相，（1）甲与乙不在两端，有多少种排法？
（2）甲、乙必须相邻，有多少种排法？（3）甲、乙之间恰好隔两人，有多少种排法？
（4）甲在乙和丙的左端，有多少种排法？
20、（9分）一个口袋内有4个不同的红球，6个不同的白球。⑴、从中任取4个球，红球的个数不比白球少的取法有多少种？⑵、若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种？
21(9分)、从7名男生5名女生中，选出5人，分别求符合下列条件的选法种数有多少种？
（1）
、
必须当选；（2）、都不当选；（3）、不全当选；（4）至少有2名女生当选；（5）选出5名同学，让他们分别担任体育委员、文娱委员等5种不同工作，但体育委员由男生担任，文娱委员由女生担任．
22．(9分)由0~5这六个数；①可组成没有重复数字的数多少个？②可组成没有重复数字的5位数中偶数多少个？③可组成没有重复数字的5位数中比24305大的数有多少个？
13 
14、
15．59___ 16. 16
17. 解:(1). 从口袋内取出3个球的取法共有
种.
(2). 从口袋内取出3个球，使其中恰有1个黑球的取法共有
种.
(3). 从口袋内取出3个球，使其中至少有1个黑球的取法共有
种.
18. 解:(1). 无重复数字的三位数
个.
(2). 无重复数字的三位奇数
个.
(3). 大于3012且无重复数字的四位数
个.
19．解（1）（特殊元素优先排）先安排甲乙二人到中间的6个位置中的两个，有
种，
其余的6个人全排列
种，所以共计：
种排法.
（2）（捆绑法）
种.
（3）（插入法、捆绑法）余下的六人中任选两人放在甲乙二人中间，有
种，甲乙二人全排，有
种，然后把这四人“捆绑”与其他四人排队，有
种， ∴共有
种.
（4）（定序相除法）8个人全排列有
种，甲乙丙三人有
种，乙丙二人有种，
∴共有
种.
20、解：⑴、将4个球分成三类情况：
①、取4个球，没有白球有
种……………………………………………2分
②、取3个红球1个白球有
种………………………………………4分
③、取2个红球2个白球有
种
∴取法共有
种……………………………6分
⑵、设取
个红球，
个白球，则
，
∴
或
或
……………………………………………………8分
∴符合题意的取法种数有
种……………12分
21. 解：（1）除、选出外，从其它10个人中再选3人，共有的选法种数为
，
（种）．
（2）去掉、，从其它10人中任选5人，共有的选法种数为：
（种）．
（3）按、的选取情况进行分类：、全不选的方法数为
，、选1人的方法数为
，共有选法
（种）．
本小题的另一解法：从12人中选5人的选法中去掉、全选的情况，所有选法只有
（种）．
方法一：按女同学的选取情况分类：
选2名女同学、3名男同学；选3名女同学2名男同学；选4名女同学1名男同学；选5名女同学．所有选法数为：
（种）．
方法二：从反面考虑，用间接方法，去掉女同学不选或选1人的情况，所有方法总数为：
（种）．
（5）选出一个男生担任体育班委，再选出1名女生担任文娱班委，剩下的10人中任取3人担任其它3个班委．用分步计数原理可得到所有方法总数为：
（种）．
22.解 ⑴
个
⑵要求是5位数,因此6个数中选5个,首位不能是0,个位必须是偶数,分为三种取法
①5位数中无0 个位有
种取法,其余有
,即共有
个
②5位数中有0 ⅰ 0在个位，共有
个，ⅱ 0不在各位 
∴共有 48+120+144=312个
⑶首位以 3，4，5开头的5为数都符合要求共计
，
其次以25开头的数有 
，
以245开头的数有
，
以243开头的数有，有4个数比24305大
∴共有360+24+6+4=394 个