高二年级数学上学期期末考试

高二年级数学上学期期末考试

数 学 试 题

本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 共120分，考试时间120分钟.

注意事项：

1．各题的答案或解答过程均写在答题纸内的指定处，写在试卷上的无效.

2．答题前，考生务必将自己的“姓名”，“班级”和“学号”写在答题纸上.

3．考试结束，只交答题纸.

第Ⅰ卷（选择题　共48分）

一、选择题（本大题共12个小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1．不等式等价于　　　　　　　　　　　　　　　　　　　　　　　　 　　（　　）

　　　 A． 　　　　 B． 　 C．　　 　　　 D．

2．如果直线  与直线平行, 那么实数a等于　　 　 （　　）

　　　 A．　　　　　　　　 B． 　　　　　　　　　C．　　  　　　　 D．

3．空间四边形的对角线互相垂直且相等，顺次连结这个空间四边形各边的中点，所组成的

四边形是　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　 （　　）

　　　 A．正方形　　　　　　　 B．矩形　　　 　　　 C．平行四边形 　　　 D．梯形

4．抛物线的焦点坐标是　　　　　　　　　　　　　　　　　　  　　　（　　）

　　　 A．(0,－4)　　　　　 B．(0,－2)　　　 　 C．　　　　　D．

5．如果一个角的两边分别垂直于另一个角的两边，那么这两个角的大小关系是　　 （　　）

　　　 A．相等　　　　　 B．互补　 　　　　　　 C．相等或互补　　　　D．不确定

6．若是互不相同的空间直线，是互不重合的两个平面，则下列命题中为真命题是　　　　　　　　　　　　　　　　　 （　　）

　　　 A．若，则 　　　B．若，则　 　　　　　

　　　 C．若，则 　　　　　　D．若，则

7．满足方程的的最大值是　　　　　　　　　 　　　　　　　 （　　）

　　　 A．　　　　　　　　B．　　　　　　　　　　 C．　 　　　　　　　 D．

8．已知点在直线上运动，则的最小值是　　　　　　　　　 （　　）

　　　 A．　　　　  　B．2 　　　　　　　　　　C．2　　　　　　　　　D．4

9．已知是一对异面直线，且成80°角，则在过空间一定点P的直线中与a，b所成角均为80°的直线有　　　　　　　　　　　　 　　　　　　　　　　　　　　　　 （　  ）

　　　 A．4条　　　　　　　　　　B．3条　　　　　　　　　 C．2条 　　　　　　　　　D． 1条

10．在△ABC中，AB=AC=10cm, BC=12cm, PA平面ABC，PA = 8cm, 则点P到边BC的

1,3,5

距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　（　　）

　　　 A．10 cm　　　　　　　 B．13 cm　 　　　　　　C．cm　　　　　　D． cm

11．关于函数的叙述不正确的是　　　　　　　　 　　（ 　 ）

　　　 A．图象关于y轴对称 　　　　　　　　　　　　　　B．值域是 　　

　　　 C．图象是椭圆的一部分 　　　　　　　　　　　　D．图象是双曲线的一部分

12．直线与曲线的交点个数是　　　　　　　　　　  　（　　）

A．0 　　　　　　　　　　　B．1 　　　　　　　　　　　C．2　 　　　　　　　　　 D．3

第Ⅱ卷（非选择题，共72分）

二、填空题（本大题共4个小题，每小题4分，共16分）

13．过抛物线的焦点，倾斜角为45°的直线被抛物线截得的弦长为　　　　 ；

14．已知双曲线的虚轴长是实轴长与焦距的等比中项，则此双曲线的离心率是　　　　  ；

15．函数 则的最大值为　　　　；

16．下面有四个命题：

①经过空间一点与两条异面直线都相交的直线有且只有一条；

②经过空间一点与两条异面直线都垂直的直线有且只有一条；

③经过空间一点与两条异面直线都平行的平面有且只有一个；

④经过空间一点与两条异面直线都垂直的平面有且只有一个．

其中真命题的序号是_______________（把符合要求的命题序号都填上）.

三、解答题（本大题共6小题，共56分，解答应写出必要的文字说明、证明过程及演算步骤）

17．（本小题满分8分）已知直线与直线的倾斜角相等，并且与两坐标轴围成的三角形的面积等于24，求直线的方程．

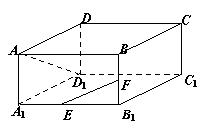18．（本小题满分8分）长方体中，分别是的中点，

求：．

19．（本小题满分10分）点P为双曲线的渐近线与右准线在第一象限内的交点，圆C与双曲线的两条渐近线都相切，且P为切点，求圆C的标准方程.

20．（本小题满分10分）如图，点P是矩形ABCD所在的平面外一点， E、F分别是AB、PC的中点．

　 （1）求证：EF∥平面PAD；

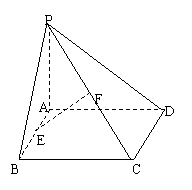　 （2）若PA⊥平面ABCD，且PA=AD，求证：EF⊥平面PCD.

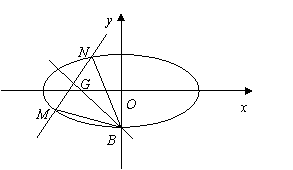
21．（本小题满分10分）已知动点与定点和定直线的距离相等．

（1）求动点M的轨迹C的方程；

（2）设M、N是轨迹C上异于原点O的两个不同点，直线OM和ON的倾斜角分别为和，当、变化，且时. 求证：直线MN恒过一定点．

22．（本小题满分10分）已知椭圆的中心为坐标原点O，其中一个焦点坐标为（，0），离心率为．

（1）求椭圆C的方程；

（2）已知向量，是否存在斜率为的直线l，l与曲线C相交于M、N两点，使向量与向量的夹角为，且? 若存在，求出k值，并写出直线l的方程；若不存在，请说明理由．

参考答案

BAABD　 BDCAC　DC

1,3,5

13．16　　　 14．　　　 15．　　16．②　

17．解：∵直线3x+4y－7=0的斜率是，

∴直线l的斜率为，设直线l的方程为.

设x=0, 得y=b;　设y=0, 得x=，

所以， ∴.

∴直线l的方程为

18．解:连结，则∥∥

即为与所成角或其补角，　　　　　　　　　　　　　　

且

 19．解：右准线方程为：x=3， 一条渐进线方程为：

所以

(1) 当圆心C在x正半轴上时,

(2) 当圆心C在y正半轴上时，

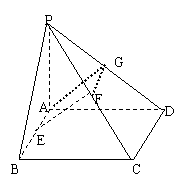
20．证明：(1)取PD的中点G联结AG，GF，

∵G，F分别是PD，

PC的中点∴GF//CD

又∵AB//CD∵AE//GF且AE=GF

∴四边形AEFG为平行四边形

∴EF//AG∵AG平面PAD

∴EF//平面PAD

(2)∵PA=AD且PG=GD∴AG⊥PD,

又∵CD⊥AD, ∵PA⊥平面ABCD,

∴CD⊥PA∵PA∩AD=A, ∴CD⊥平面PAD,

∵AG平面PAD∴AG⊥CD

∵AG//EF∴EF⊥CD,EF⊥PD

∵PD∩CD=D,∴EF⊥平面PCD

21．解：（1）由抛物线的定义可知：点M的轨迹C的方程为抛物线，所以M的轨迹C的方程为。

（2）方法1：设，，由题意得，直线MN的斜率存在，设直线去，得，由韦达定理知：　　 

当时，，

　　

可得，因此直线MN的方程为：，当时，，所以，直线MN过定点。

方法2：直线OM的方程为：y=k₁x，直线ON的方程为：y=k₂x由tanαtanβ =1可得k₁k₂=1，

，

令y=0，则

所以，直线MN过定点。

22．解：（1）∵，

∴，.

∴椭圆C的方程为：

(2)设直线l的方程为：，

设，

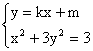，消去y，得，

………①

线段MN的中点G，

；，

线段MN的垂直平分线的方程为：

∵，

∴线段MN的垂直平分线过B（0，-1）点，

∴

∴…　　　　　　　　 ……②

②代入①，得，

解得这个不等式，得………③

∵△BMN为等边三角形，∴点B到直线MN的距离，

而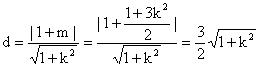

∴，

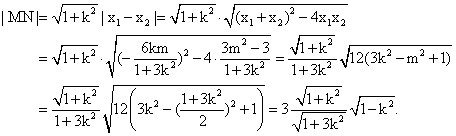
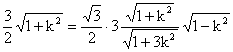解得，即，满足③式. 代入②，得.

直线l的方程为：.