高二年级数学下学期期中考试
数 学 试 题
命题人：昆明第三中学 徐青华
第I卷 选择题（选择题共36分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、学号、考试科目用铅笔涂写在机读卡上。
2．每小题选出答案后，用铅笔把机读卡上对应题目的答案标号涂黑.
3．考试结束，监考人员将第Ⅱ卷和机读卡一并收回。本试卷不收，考生妥善保管，
不得遗失。
一、选择题：(本大题共12个小题, 每小题3分，满分36分。在每小题给出的
四个选项中，只有一项是符合题目要求的.)
（1）垂直于同一条直线的两条直线一定 （ ）
A．平行 B．相交 C．异面 D．以上都有可能
（2）“
”是“直线
平行于直线
”的
（ ）
A．充分必要条件 B．必要而不充分条件
C．充分而不必要条件 D．既不充分也不必要条件
（3）一个平行于棱锥底面的截面与棱锥的底面的面积之比为1∶9，则截面把棱锥的高分成两段的长度之比为 （ ）
A． B． C． D．
（4）空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是 （ ）
A．垂直且相交 B．垂直但不相交
C．相等但不一定垂直 D．不相等也不垂直
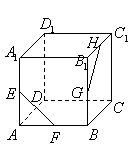（5）如图，在正方体
中，
分别为
，
，
，
的中点，则异面直线
与
所成的角等于（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
（6）若
是两条不同的直线，
是三个不同的平面，则下列命题中的真命题是（ ）
A．若
，则
B．若
，
，则
C．若
，
，则
D．若
，
，则
高二数学试卷第1页（共6页）
（7）一动圆的圆心在抛物线
上，且动圆恒与直线
相切，则此动圆必过定点（ ）
A．
B．
C．
D．
 |
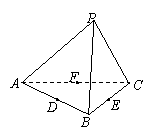（8）如图，在正四面体
中，
分别是
的中点，
则下列四个结论中不成立的是（ ）
A．
平面
B．
平面
C．平面
平面
D．平面
平面
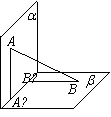（9）如图，平面a⊥平面b，A∈a，B∈b，AB与两平面a，b 所成的角
分别为
和
，过A，B分别作两平面交线的垂线，垂足为A¢，B¢，
则AB∶A¢B¢＝（ ）
A．4∶3 B．3∶
（10）半径为1的球面上的四点
是正四面体的顶点，则
与
两点间的球面距离为
（ ）
A．
B．
C．
D．
（11）设
分别是双曲线
的左、右焦点，若双曲线上存在点，使
且
，则双曲线的离心率为 （ ）
A．
B．
C．
D．
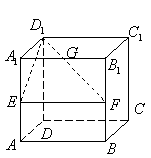
（12）在棱长为1的正方体
中，
分别为棱
的中点，
为棱
上的一点，且
．则点到平面
的距离为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
高二数学试卷第2页（共6页）
数 学 试 题
命题人：昆明第三中学 徐青华
第II卷（非选择题共64分）
注意事项：
1． 第II卷共4页，用钢笔或圆珠笔直接答在试题卷上。
2． 答卷前将班级、姓名、学号等项目填写清楚。
3． 考试结束，监考人员将本卷和机读卡一并收回。
|
题 号 |
一 |
二 | 三 |
总 分 | |||
| 19 | 20 | 21 | 22 | ||||
| 得 分 |
|
|
|
|
|
|
|
二、填空题：（本大题共6小题；每小题3分，共18分，把答案填在题中横线上。）
（13）已知某球的体积与其表面积的数值相等，则此球体的体积为 ______________．
（14）方程
表示焦点在y轴上的椭圆，则m的取值范围是 ．
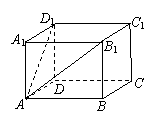（15）如图，长方体
中，
，
则长方体的对角线
长等于 ________．
（16）以双曲线
的右焦点为圆心，且与其渐近线相切的圆的方程是_______________．
（17）如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 ．
（18）经过抛物线
的焦点
作与对称轴垂直的直线, 交抛物线于
、
两点,
是抛物线的顶点,再将直角坐标平面沿
轴折成直二面角, 此时∠
的余弦值是
．
高二数学试卷第3页（共6页）
三、解答题：(本大题共4小题；共46分，解答应写出文字说明、证明或演算步骤。)
得 分 评卷人 （19）（本小题满分10分）
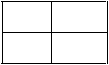
已知ABCD是正方形，PA⊥平面ABCD，且PA=AB=
，E、F是侧棱PD、PC上的点，且
.
（1）求证：EF∥平面PAB ；
（2）求直线PC与底面ABCD所成角
的正切值；
得 分 评卷人 （20）（本小题满分12分）
已知直线
与椭圆
相交于
两点.
（1）若椭圆的离心率为
，焦距为2，求线段
的长；
（2）在（1）的椭圆中，设椭圆的左焦点为
，求△
的面积。
高二数学试卷第4页（共6页）
得 分 评卷人 （21）（本小题满分12分）
 | |||
 | |||
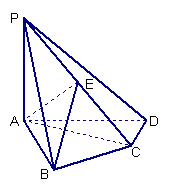
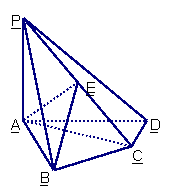如图，四棱锥
中，
底面
，
，
，
，
，
是
的中点．
（1）求证：
面
；
（2）求二面角
的平面角的正弦值．
高二数学试卷第5页（共6页）
得 分 评卷人 （22）（本小题满分12分）
已知椭圆
的方程是
，双曲线
的左、右焦点分别是的左、右顶点，双曲线的左、右顶点分别是的左、右焦点．
（1）求双曲线的方程；
（2）若直线
与双曲线有两个不同的交点
，且
（
为原点），求实数
的取值范围．
高二数学试卷第6页（共6页）
数学试题参考解答
一、选择题：本题考查基础知识和基础运算。每小题3分，满分36分.
（1）D；（2）A；（3）D；（4）B；（5）B；（6）C；
（7）A；（8）D；（9）C；（10）C；（11）B；（12）D。
二、填空题：本题考查基本知识和基本运算。每小题3分，满分18分。
（13）
；（14）8＜m＜25；（15）3；（16）
；（17）36；（18）
.
三、解答题(本大题共4个题, 第19题10分，其余各题均为12分，满分46分):
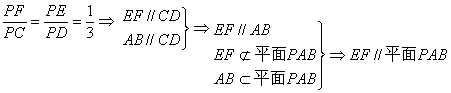19．证明：（1）
 |
证明：（2）连结AC，因为PA
平面ABCD，所以
就为直线PC与平面ABCD所成的角。即
又因为正方形ABCD的边长为，所以AC=
，
所以 
20．解：（1）
∴椭圆的方程为
, 联立
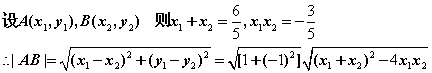
（2）由（1）可知椭圆的左焦点坐标为F1（-1，0），直线AB的方程为x+y-1=0,
所以点F1到直线AB的距离d=
,
又AB=
， ∴△ABF1的面积S=
=
21．（1）证明：底面，
又
，
，故
面
面，故
又，，故
是的中点，故
从而
面
，故
易知
，故面
（2）过点作
，垂足为
，连结．
由（2）知，面，故
是二面角的一个平面角．设
，则
，
，
从而
，故
．
22．解：（1）由题意知，椭圆焦点为
，顶点
．
所以双曲线中，
，故双曲线的方程为
．
（2）联立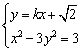
得，
．由题意知，
得
①
记
，则
．
，由题，
知
，
整理得
②
由①②知，
，故的取值范围是
．