高二年级数学九校期中联考试卷
数 学 2008.4
命题单位:鲁山一高 命题人:李慧卿 校对人:梁艳军
注意事项:本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共8页,三道大题,共22 小题。满分150分,考试时间120分钟。
第I卷(选择题共60分)
一、选择题:本大题共有12小题,每小题5分,共60分。在每小题给出的四个选项中有且只有一项是符合题目要求的。
1.空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为( )
A.3 B.1或
2.已知直线![]() 与平面
与平面![]() 所成的角为30°,b是
所成的角为30°,b是![]() 内的任一直线,则
内的任一直线,则![]() 与b所成的角中最大的为( )
与b所成的角中最大的为( )
A.30° B.90° C.150° D.180°
3.已知直线a,b异面,直线b,c异面,则直线a,c的位置关系为( )
A.平行 B.相交 C.异面 D.以上均有可能
4.无论怎样选择平面,两条异面直线在该平面内的射影都不可能是( )
 A.两条平行线 B.两条相交线
A.两条平行线 B.两条相交线
C.一条直线和直线外一点 D.两个点
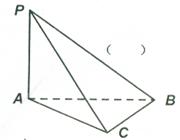
5.如图,PA上平面ABC,△ABC中,BC⊥AC,则△PBC是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
6.已知直线m与平面α,β, m![]() α,则α∥β是m∥β( )
α,则α∥β是m∥β( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要
7.6名学生报名参加5项体育比赛,每人限报一项,报名方法共有( )种
A.65 B.![]() D.
D.![]()
8.k∈N+,且k≤40,则(50—k)(51—k)(52—k)…(79—k)用排列数符号表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.正方体的外接球的体积为36![]() ,则正方体的棱长为( )
,则正方体的棱长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在120°的二面角的棱上,有两个点A、B,AC、BD分别是这两个二面角的两个面内垂直于AB的线段,已知AB=6cm,AC=2cm,BD=4cm,则CD长为( )
A.![]() cm B.8cm C.
cm B.8cm C.![]() cm D.
cm D.![]() cm
cm
1l.以三棱柱的六个顶点中的四个顶点为顶点的三棱锥有( )
A.18个 B.15个 C.12个 D.9个
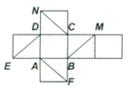 12.如图是正方体的平面展开图,在这个正方体中,有:①BM与ED平行:②CN与BE是异面直线;③CN与BM成60°;④DM与BN垂直。以上四个命题中,正确命题的序号是:( )
12.如图是正方体的平面展开图,在这个正方体中,有:①BM与ED平行:②CN与BE是异面直线;③CN与BM成60°;④DM与BN垂直。以上四个命题中,正确命题的序号是:( )
A.①②③ B.②④ C.③④ D.②③④
第II卷(非选择题共90分)
二、填空题(共4小题,每小题4分,共1 6分)
13.设地球半径为R,在北纬60°圈上有甲、乙两地,它们在纬线圈上的弧长为![]() ,则这两地的球面距离为
,则这两地的球面距离为
14.甲、乙、丙、丁四人排成一排,则甲、乙二人之间恰好排有一人排法种数为 。
15.在长方体ABCD—A1B1C1D1的六个表面中,从顶点A出发的三个面的面积分别为2、3、6,则长方体的对角线B1D1长等于 。
16.已知正三棱锥的底面边长为6cm,侧棱长为4cm,则正三棱锥底面上的高长为 。
三、解答题(共6大题)
17.(本题满分12分)有6名同学站成一排,求:
(1)甲不站排头也不站排尾有多少种不同的排法;
(2)甲不站排头,且乙不站排尾有多少种不同的排法;
(3)甲、乙、丙不相邻有多少种不同的排法。
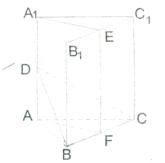 18.(本题满分12分)正三棱柱ABC—A1B1C1中,BC=2,AA1=
18.(本题满分12分)正三棱柱ABC—A1B1C1中,BC=2,AA1=![]() ,D、E分别是AA1、B1C1的中点。
,D、E分别是AA1、B1C1的中点。
(1)求证:面AA1E⊥面BCD;
(2)求二面角D—BC—A的大小。
19.(本题满分12分)10人中有7人会说英语,6人会说德语(每人至少会其中一种),现要选出6人去完成一项任务,要求3人会说英语,3人会说德语,求有多少种选法.
20.(本题满分12分)C64分子是与C60分子类似的球状多面体结构,它有64个顶点,以每个顶点为一端点都有3条棱,各面是四边形或六边形,求C64分子中四边形和六边形的个数。
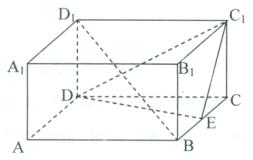 21.(本题满分12分)如图,ABCD——A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点,
21.(本题满分12分)如图,ABCD——A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点,
(1)求异面直线AC1和DE所成角的大小;
(2)求异面直线AC1和DE的距离。
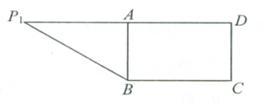
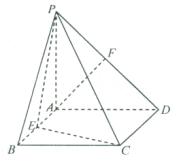 22.(本题满分14分)在直角梯形P1DCB中,P1D∥BC,
22.(本题满分14分)在直角梯形P1DCB中,P1D∥BC,![]() 且
且![]() ,
,![]() ,
,![]() ,A是
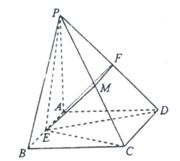
,A是![]() 的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P—CD—B成45°角,设E、F分别是线段AB、PB的中点。
的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P—CD—B成45°角,设E、F分别是线段AB、PB的中点。
(1)求证:AF∥平面PEC;
(2)求PD与平面ABCD所成角的大小;
(3)求点D到平面PEC的距离。
高二数学联考试题答案
一 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | D | D | B | A | B | C | B | B | C | C |
二 填空题
13.![]() 14.8 15.
14.8 15.![]() 16.2cm
16.2cm
三.解答题
17.解:(1)甲不站排头也不站排尾可以有:![]() 种,其余的人共有:
种,其余的人共有:![]() 种站法所以甲不站排头也不站排尾共有
种站法所以甲不站排头也不站排尾共有![]()
![]() =480一——4分
=480一——4分
(2)甲站排头共有![]() 种,乙站排尾共有
种,乙站排尾共有![]() 种站法
种站法
甲站排头且乙站排尾共有![]() 种站法,六人站一排共有
种站法,六人站一排共有![]() 种站法
种站法
甲不站排头乙不站排尾共有![]() —2
—2![]() +
+![]() =504种站法———4分
=504种站法———4分
(3)除甲乙丙之外的三人共有![]() 种站法甲乙丙就有
种站法甲乙丙就有![]() 种站法
种站法
所以甲乙丙不相邻共有共有![]()
![]() =144种站法————4分
=144种站法————4分
18.(1)略——6分 (2)![]() ——6分
——6分
19.解法一:选3人会英语3人会德语共分有以下几种情况:
选3人只会讲英语去讲英语的有![]() 种——2分
种——2分
选2人只会讲英语1人即会讲英语又会讲德语去讲英语的有![]() 种2分
种2分
选1人只会讲英语2人即会讲英语又会讲德语去讲英语的有![]() 种2分
种2分
选3人即会讲英语又会讲德语去讲英语的有![]() 种————2分
种————2分
所以选6人完成这项任务共有![]() +
+![]() +
+![]() +
+![]() =309——4分
=309——4分
另解:选3人会英语3人会德语共分有以下几种情况:
选3人只会讲德语去讲德语的有![]() =35种——2分
=35种——2分
选2人只会讲德语1人即会讲英语又会讲德语去讲德语的有![]() =180种2分
=180种2分
选1人只会讲德语2人即会讲英语又会讲德语去讲德语的有![]() =90种2分
=90种2分
选3人即会讲英语又会讲德语去讲德语的有![]() =4种2分
=4种2分
所以选6人完成这项任务共有![]() +
+![]() +
+![]() +
+![]() =309种一—4分
=309种一—4分
20.解:设C64分子中四边形和六边形的个数分别为x个、Y个————2分
C64分子多面体顶点数V=64,面数F=x+y,棱数E=(3×64)÷2一一2分
根据欧拉公式,可得64+x+y一![]() (3×64)=2(1) ————2分
(3×64)=2(1) ————2分
另一方面,根据棱数可得2E=3×64=4x+6y(2)————————2分
有(1)(2)得x=6,y=28——————————————————3分
C64分子中四边形有6个和六边形有28个———————————1分
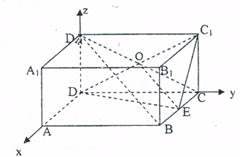 21、(1)如图:分别以DA、DC、DDl为x轴、y轴、z轴,建立空间直角坐标系D—xyz,则A(2,0,0)Cl(0,2,1)D(0,0,0)E(1,2,0)
21、(1)如图:分别以DA、DC、DDl为x轴、y轴、z轴,建立空间直角坐标系D—xyz,则A(2,0,0)Cl(0,2,1)D(0,0,0)E(1,2,0)
∴![]() (—2,2,1)
(—2,2,1)![]() (1,2,0),
(1,2,0),
![]()
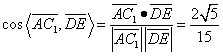
∴异面直线ACl和DE所成角的大小为![]() 。————————6分
。————————6分
(2)由(2)知![]() (—2,2,1)
(—2,2,1)![]() (1,2,0),设与
(1,2,0),设与![]() ,
,![]() 都垂直的向量为
都垂直的向量为![]() (x,y,z)
(x,y,z)
则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]()
![]()
令x=2则y=l,z=6 则有![]() =(2,一1,6),又
=(2,一1,6),又![]() =(2,0,0)
=(2,0,0)
∴异面直线AC1和 DE距离为:
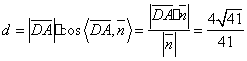 ——————————6分
——————————6分
22法一:(1)取PC中点M,连结FM,EM
∵F、M分别为PD、PC中点 ∴![]()
∵E为AB中点, ∴![]()
∴![]() ,∴FMEA为平行四边形∴AF//EM………3分
,∴FMEA为平行四边形∴AF//EM………3分
又∵AF![]() 平面PEC,EM
平面PEC,EM![]() 平面PEC∴AF//平面PEC.…………………4分
平面PEC∴AF//平面PEC.…………………4分
(2)∵![]() ∴
∴![]()
∵AB//DC ∴![]() ∴DC⊥PD DC⊥AD
∴DC⊥PD DC⊥AD
∴∠PDA为二面角P—CD—B的平面角,即∠PDA=45°…………………7分
又∵PA=AD=3 ∴PA⊥AD ∴PA⊥平面ABCD
∴PD与平面ABCD所成角为∠PDA=45°……………………………………9分
(3)连结ED, ∵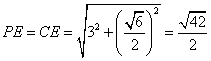 ,M为PC中点 ∴EM⊥PC‥10分
,M为PC中点 ∴EM⊥PC‥10分
由(I)知![]() ,
,![]()
∴![]() ………………………………12分
………………………………12分
设点D到平面PCE的距离为d,由![]()
![]() ∴
∴![]() 即点D到平面PEC的距离为
即点D到平面PEC的距离为![]() ………14分
………14分
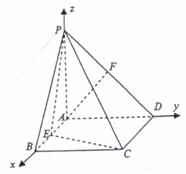 解法二:
解法二:
∵![]() ∴
∴![]()
∵AB//DC ∴![]() ∴DC⊥PD DC⊥AD
∴DC⊥PD DC⊥AD
∴∠PDA为二面角P—CD—B的平面角,即∠PDA=45°
又∵PA=AD=3 ∴PA⊥AD
以A为原点,AB为x轴,AD为Y轴,AB为z轴,建立空间直角坐标系A—xyz………3分
则P(0,0,3),D(0,3,0),F(0,![]() ,
,![]() ),C(
),C(![]() ,3,0),(
,3,0),(![]() ,0,0)
,0,0)
∴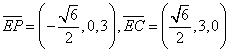 ………6分
………6分
设![]() =(x,y,z)为平面PEC的一个法向量,由
=(x,y,z)为平面PEC的一个法向量,由![]() 得:
得:
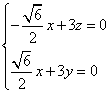 取
取![]() ………………………8分
………………………8分
(1)∵![]() ∴
∴![]() ,∴AF与平面所成角为0°
,∴AF与平面所成角为0°
又∵A![]() 平面PEC ∴AF
平面PEC ∴AF![]() 面PEC,∴AF//平面PEC……………………10分
面PEC,∴AF//平面PEC……………………10分
(2)∵![]() =(0,3,一3),
=(0,3,一3),![]() =(0,0,3)为平面ABCD的一个法向量
=(0,0,3)为平面ABCD的一个法向量
PD与平面ABCD所成角为![]() 则
则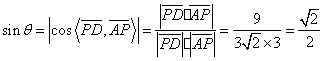
∴PD与平面ABCD所成角为45°……………………………………………………12分
(3)∵![]() ,∴D到平面PEC的距离
,∴D到平面PEC的距离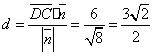 …14分
…14分
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
|
|
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||