高二年级数学学科第二学期期终试卷(答案)
一、填空题(本大题满分为36分,共有12题,每题3分)
1、计算![]() ___________答案1
___________答案1
2、已知直线方程![]() ,则它的斜率是_________答案
,则它的斜率是_________答案![]()
3、已知总体方差![]() ,则总体平均数为________答案
,则总体平均数为________答案![]()
4、若方程![]() 表示双曲线,则实数
表示双曲线,则实数![]() 的取值范围是______________答案
的取值范围是______________答案![]()
5、已知复数![]() 满足
满足![]() ,则
,则![]() 的最大值为__________答案
的最大值为__________答案![]()
6、以椭圆![]() 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线![]() 的两条渐近线都相切的圆方程_________________________答案
的两条渐近线都相切的圆方程_________________________答案![]()
7、在5名男同学和4名女同学中选出3人参加社区服务,要求3名学生中必须男女生都有的选法有____________种 答案70
8、已知![]() ,则
,则![]() ______________答案-1
______________答案-1
9、由![]() 这7个数字组成没有重复数字的三位数中,能被5整除的数的概率为__________答案
这7个数字组成没有重复数字的三位数中,能被5整除的数的概率为__________答案![]()
10、若复数z=![]() ,则
,则![]() _________答案100
_________答案100
11、有三位学生等可能地选择A、B、C、D四种不同的数学参考资料中的一种,则三位学生选择的数学参考资料互不相同的概率为___________答案![]()
12、若椭圆![]() 上的一点
上的一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是坐标原点,则
是坐标原点,则![]() _________答案3
_________答案3
二、选择题(本大题满分为12分,共有4题,每题3分)
13、抛物线![]() 的焦点坐标是( )B
的焦点坐标是( )B
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14、两个虚数![]() 互为共轭的充要条件是( )D
互为共轭的充要条件是( )D
(A)![]() (B)
(B)![]()
(C)![]() (D)向量
(D)向量![]() 关于
关于![]() 轴对称
轴对称
15、使复数![]() 为实数的充分不必要条件是( )D
为实数的充分不必要条件是( )D
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
16、已知复数![]() 满足:
满足:![]() ,则它在复平面上对应点的轨迹是( )A
,则它在复平面上对应点的轨迹是( )A
(A)线段 (B)圆 (C)椭圆 (D)双曲线
三、解答题(本大题满分52分,共有5题,解答下列各题必须写出必要的步骤)
17、(本题满分8分)已知![]() ,求
,求![]() 的值.
的值.
解:![]() ,
,![]() ----------------------------------3分
----------------------------------3分
![]() ,
,![]() ,
,![]() -------------------------------------2分
-------------------------------------2分
![]() ,
,![]() ,
,![]() ------------------------------------2分
------------------------------------2分
![]() -------------------------------------------------------------1分
-------------------------------------------------------------1分
18、(本题满分10分)已知复数![]() ,当
,当![]() 为何实数时,复数
为何实数时,复数![]() 对应点在直线
对应点在直线![]() 上.
上.
解:![]() ---------------------------3分
---------------------------3分
![]() -----------------------------------3分
-----------------------------------3分
![]() ,
,![]() ,
,![]() ---------------3分
---------------3分
经检验![]() -------------------------------------------------------------1分
-------------------------------------------------------------1分
19、(本题满分10分)已知关于![]() 的方程
的方程![]() 有实根,求
有实根,求![]() 的值及方程的两根.
的值及方程的两根.
解:设实根为![]() --------------------------------------------------------------------1分
--------------------------------------------------------------------1分
![]()
![]() ------------------------------------------------2分
------------------------------------------------2分
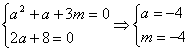 ----------------------------------------------4分
----------------------------------------------4分
![]() ,
,![]() -------------------------------2分
-------------------------------2分
![]() ------------------------------------------1分
------------------------------------------1分
20、(本题满分12分)已知直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
解:设![]()
(1)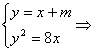
![]() ------------------------------1分
------------------------------1分
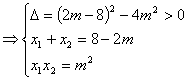 -----------------------------------------------2分
-----------------------------------------------2分
![]() ,
,![]() ----2分
----2分
![]() ,
,![]() ---------------------------------------------------------1分
---------------------------------------------------------1分
(2) ![]() ,
,![]() ------------------------------------1分
------------------------------------1分
![]() ,
,
![]() -----------------------------------------2分
-----------------------------------------2分
![]() ,
,
![]() ,
,![]() ,---------------------------------2分
,---------------------------------2分
经检验![]() ------------------------------------------------------------1分
------------------------------------------------------------1分
21、(本题满分12分)已知点![]() 和圆
和圆![]() ,点
,点![]() 在圆
在圆![]() 上运动,点
上运动,点![]() 在半径
在半径![]() 上,且
上,且![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)求动点![]() 到定点
到定点![]() 的距离的最小值.
的距离的最小值.
解:(1)![]() ------------------------2分
------------------------2分
![]() -----------------------------------------------2分
-----------------------------------------------2分
动点![]() 的轨迹方程:
的轨迹方程:![]() --------------------------------2分
--------------------------------2分
(2)![]()
![]() -------------------1分
-------------------1分
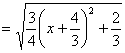 -------------------------------------------2分
-------------------------------------------2分
![]() -----------------------------------------------------1分
-----------------------------------------------------1分
![]() 时,
时,![]() -------------------------------------2分
-------------------------------------2分