高二年级数学第二学期期中考试
数 学 试 卷（理）
总分：150分 时量：120分钟
第Ⅰ卷（选择题 共55分）
一、选择题（本大题共11小题，每小题5分，共55分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．
的虚部为( )
A．
B．
C．
D．
2．用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（ ）．
A．假设三内角都不大于60度 B．假设三内角都大于60度
C．假设三内角至多有一个大于60度 D．假设三内角至多有两个大于60度
3．
的值为（ ）
A．0 B． 
C．2 D．4
4．函数
的单调减区间是
A．（
B.
C．（， D.
5．直线
与抛物线
所围成的图形面积是
（ ）
A．20 B．
C．
D． 
6．若函数
在R上是一个可导函数，则
在R上恒成立是在区间
内递增的
A．充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
7.函数
的图象如图所示，则导函数
的图象可能是
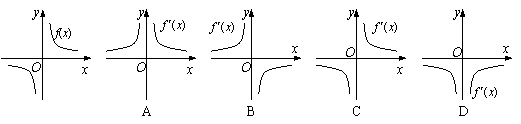
8．已知
,则
等于( )
A．
B．
C．
D．
9．f (x)是定义在(0,+∞)上的非负可导函数
，且满足
，对任意的正数
a ﹑b ，若a ＜ b，则必有 （ ）
A．a f (a)≤b f (b) B．a f (a)≥b f (b) C．a f (b)≤b f (a) D．a f (b)≥b f (a)
10．设
是定义在正整数集上的函数，且满足：“当
成立时，总可推出
成立”，那么，下列命题总成立的是
A．若
成立，则当
时，均有成立
B．若
成立，则当
时，均有成立
C．若
成立，则当
时，均有
成立
D．若
成立，则当
时，均有成立
11．
分别是定义在R上的奇函数和偶函数，当
时，
且
的解集为 （ ）
A．（－2，0）∪（2，+∞） B．（－2，0）∪（0，2）
C．（－∞，－2）∪（2，+∞）YCY D．（－∞，－2）∪（0，2）
数 学 试 卷（理）
第Ⅱ卷（非选择题 共95分）
二、填空题：(本大题共4小题，每小题4分，共16分．把答案填在答题卡相应位置上)
12. 若
是锐角
的一个内角，且
，则=
。
13.Q是曲线C：f(x)=e
上的动点，当Q无限趋近于点P（0，1）时，割线PQ的斜率无限接近于一个常数是___________
14． 
，经计算的
，推测当
时，有_______．
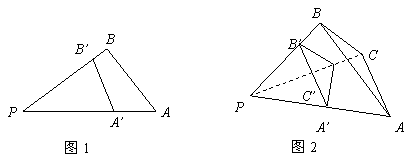
15．由图（1）有面积关系：
，则由图（2）有体积关系：
＝
．
三、解答题（本大题共6小题，共79分。解答应写出文字说明、证明过程或演算步骤）
16．求曲线
与
轴所围成的图形的面积．
17．已知函数
，若函数在其定义域内为单调函数，求
的取值范围；
18．（本题14分）
记z的共轭复数为
，是否存在复数
使等式
成立.若存在，求出满足要求的；若不存在，请说明理由.
19．观察以下各等式：
，
分析上述各式的共同特点，猜想出反映一般规律的等式，并对等式的正确性作出证明．
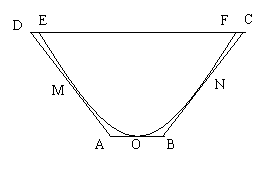
20、如图,一水渠的横断面是抛物线形，O是抛物线的顶点,口宽EF=
（1） 建立适当的直角坐标系，求抛物线方程.
（2） 现将水渠横断面改造成等腰梯形ABCD，要求高度不变，只挖土，不填土，求梯形ABCD的下底AB多大时，所挖的土最少？
参考答案
一．DBCDC ADCCD A
二．12.
13. _1 14. 
15. 
三．
16．（12分）
解：首先求出函数的零点：
，
，
.又易判断出在
内，图形在轴下方，在
内，图形在轴上方，
所以所求面积为
17．（13分）
解： 
要使函数在定义域
内为单调函数，则在内
恒大于0或恒小于0，
当
在内恒成立；
当
要使
恒成立，则
，解得
所以的取值范围为或
18．（13分）
证明：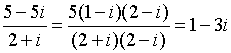
………………2分
设存在
满足要求，则
………………3分
…………………………7分
∴原方程化为：
∴
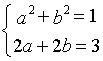…………………………10
…………12分
∴方程①无解……………………………………13分
从而原方程在复数范围内无解．………………14分
19．（14分）
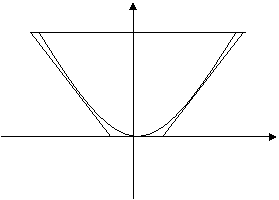
猜想：
证明：
|
|
|
|
|
|
|
|
|
|
（1）解：如图 以O为原点，AB所在的直线
|
则F（2，3），设抛物线的方程是
因为点F在抛物线上，所以
，所以抛物线的方程是
……………………6分
(2) 解：等腰梯形ABCD中,AB∥CD，线段AB的中点O是抛物线的顶点，AD，AB，BC分别与抛物线切于点M，O，N
，设
，
，则抛物线在N处的切线方程是
，所以
，……………………8分
梯形ABCD的面积是
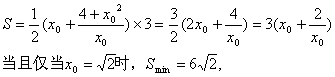……………………12分
答：梯形ABCD的下底AB=
米时，所挖的土最少.14分
