高二年级数学第二学期期中考试
数 学 试 卷（文）
总分：150分 时量：120分钟
参考公式：
用最小二乘法求线性回归方程系数公式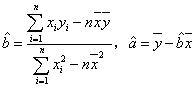
．
第Ⅰ卷（选择题 共55分）
一、选择题（本大题共11小题，每小题5分，共55分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1.
是复数
为纯虚数的（ ）
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要
2. 已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是( )
A.
=1.23x＋4 B. =1.23x+=1.23x+0.08 D. =0.08x+1.23
3.如果数列
是等差数列，则（ ）
A.
B. 
C.
D.
4.有这样一段演绎推理：“有些有理数是真分数，整数是有理数，则整数是真分数”，结论显然是错误的，是因为（ ）
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
5、用反证法证明命题“如果
”时，假设的内容应是（ ）
(A) 
(B) 
(C) 
(D) 
6、设集合A＝
，B＝
，若A
B，则a的取值范围是（
）
A．a
1 B．a<
2
7. 已知某种子的发芽率为
, 现随机种下这样的种子3粒,则恰好有2粒发芽的概率为
8、若函数f(x)＝ax＋b(a
0)有一个零点是－2，则函数g(x)＝bx2－ax的零点是（ ）
A．2，0 B．2，
C．0， D．0，
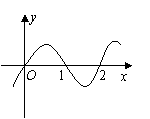9．已知函数
的图象如图所示，则有（ ）
A．b<0 B．0<b<1
C．1<b<2 D．b>2
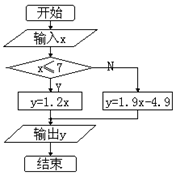
10．根据右边程序框图，当输入10时，输出的是（ ）
A．12 B．19 C．14.1 D．-30
11．设
是定义在正整数集上的函数，且满足：“当
成立时，总可推出
成立”，那么，下列命题总成立的是
A．若
成立，则当
时，均有成立
B．若
成立，则当
时，均有成立
C．若
成立，则当
时，均有
成立
D．若
成立，则当
时，均有成立
高二年级期中考试
数 学 试 卷（文）
第Ⅱ卷（非选择题 共95分）
一、选择题（本大题共11小题，每小题5分，共55分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
二、填空题：(本大题共4小题，每小题4分，共16分．把答案填在相应位置上)
12．流程图是用来描述具有 特征的动态过程；结构图是一种描述 结构的图示。
13. 在复平面内，平行四边形ABCD的三个顶点A、B、C对应的复数分别是1+3i,-i,2+i,则点D对应的复数为 。
14. 回归直线方程为y=0.5x-0.81，则x=25时，y的估计值为
15、已知数列
的通项公式
，记
，试通过计算
的值，推测出
三、解答题（本大题共6小题，共79分。解答应写出文字说明、证明过程或演算步骤）
16、(本题满分12分)
若a＞0,b＞0,求证：
17. (本题满分12分)
已知
，且 
，求z．
18、（本小题满分14分）
设甲、乙两人每次射击命中目标的概率分别为
，且各次射击相互独立。
（Ⅰ）若甲、乙各射击一次，求甲命中但乙未命中目标的概率；
（Ⅱ）若甲、乙各射击两次，求两人命中目标的次数相等的概率。
19．（14分）观察以下各等式：
，
分析上述各式的共同特点，猜想出反映一般规律的等式，并对等式的正确性作出证明．
猜想：
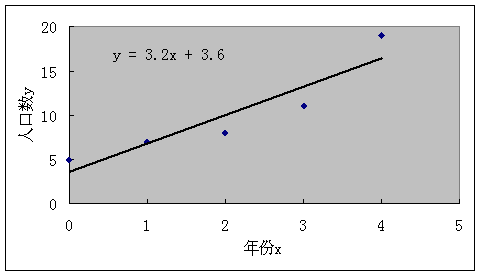
20、(本题满分14分) 某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
| 年份200x（年） | 0 | 1 | 2 | 3 | 4 |
| 人口数y（十）万 | 5 | 7 | 8 | 11 | 19 |
(1)请画出上表数据的散点图；
(2)请根据上表提供的数据，求最小二乘法求出Y关于x的线性回归方程Y=bx+a；
(3) 据此估计2005年.该 城市人口总数。
(参考数值：0×5+1×7+2×8+3×11+4×19=132，
，公式见卷首)
21．（15分）对于区间[a, b]，若函数y=f(x)同时满足下列两个条件：①函数y=f(x)在[a, b]上是单调函数；②函数y=f(x)，x∈[a, b]的值域是[a, b]，则称区间[a, b]为函数y=f(x)的“保值”区间．
（1）写出函数y=x2的“保值”区间；
（2）函数y=x2+m(m≠0)是否存在“保值”区间？若存在，求出相应的实数m的取值范围；若不存在，试说明理由．
参考答案
一．BCBCC BADAC D
二．12.时间 系统
13.
14. 11.96 15. 
16.（12分）证明：
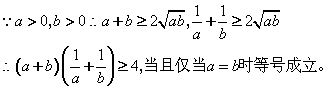
17．（12分）解：本题主要考查复数相等的充要条件及指数方程，对数方程的解法．
∵ ，∴
，∴
，
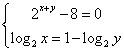解得
或
, ∴ z＝2＋i或z＝1＋2i
18.14分） 解：（Ⅰ）设A表示甲命中目标，B表示乙命中目标，则A、B相互独立，且P（A）＝
，从而甲命中但乙未命中目标的概率为
------------------------（6分）
（Ⅱ）设A1表示甲在两次射击中恰好命中k次，B1表示乙有两次射击中恰好命中l次。依题意有
由独立性知两人命中次数相等的概率为
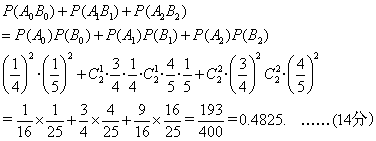
19．（14分）猜想：
证明：
20（14分）解：（1）
………………6分
（2）
，0×5+1×7+2×8+3×11+4×19=132， 
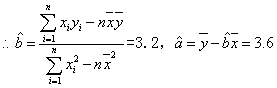
故Y关于x的线性回归方程为 y=3.2x+3.6 12分
（3）x=5,y=196(万)
据此估计2005年.该 城市人口总数196(万) 14分
21．(15分)解：（1）∵y=x2, ∴y≥0又y=x2在[a, b]上的值域是[a, b]，故[a, b]
[0，+∞
，∴a≥0，故y=x2在[a, b]上单调递增，故有
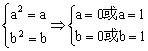，又a<b，∴
，∴y=x2的保值区间是[0，1]． …6分
（2）若y=x2+m存在“保值”区间，则应有：
i.
若a<b≤0，此时y=x2+m在[a, b]上单调递减，∴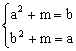
，∴a-b2=b-a2，∴(a-b)+(a2-b2)=0, ∴(a-b)(a+b+1)=0, ∴a=b(舍去)或a+b+1=0，∴a=-b-1，又
，∴-
<b≤0，又m=b-a2=b-(-b-1)2=b-b2-2b-1=-b2-b-1=-(b+)2+
-1=-(b+)2-
(-<b≤0)，∴-1≤m<-．…10分
ii.
若b>a≥0，则有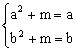
等价于方程x2-x=-m(x≥0)有两个不相等的根，∴-m=(x-)2-(x≥0)，由图象知：-<-m≤0, ∴0≤m<，又∵m≠0，∴0<m<．…14分
综上所述，函数y=x2+m存在保值区间，此时m的取值范围是0<m<或-1≤m<-．
…15分