高二年级文科数学双周测试卷
（实验班附加题必做，其它班附加题选做） 命题：黄鹤飞
一、选择题：（每小题5分，共60分）
1.老师为研究男女同学数学学习的差异情况，对某班50名同学（其中男同学30名，女同学20名）采取分层抽样的方法，抽取一个样本容量为10的样本进行研究，某女同学甲被抽到的概率为（ ）
A.
B.
C.
D.
2. 若曲线
的一条切线
与直线
垂直，则的方程为（ ）
A．
B．
C．
D．
3.已知函数
,(
)上任一点(
,
)处的切线斜率为k=
，则该函数的单调递减区间为( )
A 
B 
C 
和（1 2） D
4.若
的展开式中第二项小于第一项，且不小于第三项，则
的取值范围是( )
A．>－ B．≥－ C．－≤≤0 D．－<≤0
5.点P在曲线y = 
上移动时，过点P的切线的倾斜角的取值范围是( )
A． [0，π）
B、（0，
）∪[
，π） C．[0，）∪（，] D、[0，）∪[，π）
|
A．120种 B．48种 C．36种 D．18种
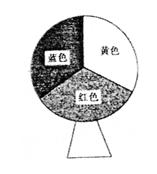
7.某风景区有一个三色风车如图（红、黄、蓝每一部分各占风车所在圆的
），已知风车设定的程序
是向左转或向右转（每次均转120°即停），而且逆时针方向转的概率是顺时针方向转的概率的2倍，
如图，假设红色在下边，则转三次之后蓝色在下边的概率是（ ）
A．
B． C．
D．
8.只用1，2，3三个数字组成一个四位数，规定这三个数必须同时使用，且同一数字
不能相邻出现，这样的四位数有（ ）
A.6个 B.9个 C.18个 D.36个
9.已知
那么
的展开式中含
项的系数是（ ）
A.15 B
9.
，则
等于( )
A.
B.
C.
D.
n（n＋1）
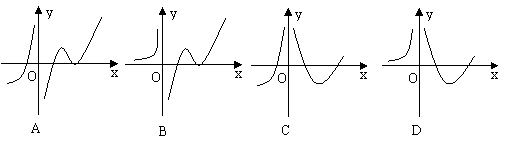
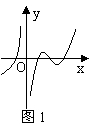11.设函数f(x)在定义域内可导，y=f(x)的图象如图1所示，则导函数y=f ¢(x)的图象可能为（ ）
12.将号码分别为1、2…9的九个小球放入一个袋中，这些小球仅号码不同，其余完全相同，甲从袋中摸出一个球，其号码为a，放回后，乙从此袋中再摸出一个球，其号码为b，则便不等式
成立的事件发生的概率等于 （ ）
A．
B．
C．
D．
二、填空题：（每小题4分，共16分）
13.
的展开式中,
的系数为
14.若在二项式
的展开式中,任取一项,则该项的系数为奇数的概率为＿＿＿
15.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有
16.若函数
在区间
上无实数根，则函数
的递减区间是
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
三、解答题：
17.(本小题10分)有6件产品，其中含有3件次品，现逐个抽取检查不放回，求：
（1）前4次恰好抽出2件次品的概率；（2）第五次恰好查出全部次品的概率
18. (本小题10分) 已知（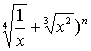
展开式中倒数第三项的系数为45。
求：（1）含
；（2）系数最大的项。
19. (本小题12分) 已知函数
的图象过点P（0，2），且在点M
处的切线方程为
．（Ⅰ）求函数
的解析式；（Ⅱ）求函数的单调区间．
20. (本小题12分)设
，点
是函数
与
的图象的一个公共点，两函数的图象在点
处有相同的切线..
（1）用
表示
（2）若函数
在（－1，3）上单调递减，求的取值范围.
21. (附加题:本题满分15分)甲、乙、丙三个同学一起参加某高校组织的自主招生考试，考试分笔试和面试两部分，笔试和面试均合格者将成为该高校的预录取生（可在高考中加分录取），两次考试过程相互独立．根据甲、乙、丙三个同学的平时成绩分析，甲、乙、丙三个同学能通过笔试的概率分别是0.6，0.5，0.4，能通过面试的概率分别是0.5，0.6，0.75．
（1）求甲、乙、丙三个同学中恰有一人通过笔试的概率；
（2）设经过两次考试后，能被该高校至少预录取两人的概率;
22.(附加题:本题满分15分)已知
是定义在R上的函数，其图象交x轴于A，B，C三点，若点B的坐标为（2，0），且
在
和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性．
（1）求
的值；
（2）在函数的图象上是否存在一点
，使得在点
的切线斜率为
？若存在，求出点的坐标；若不存在，说明理由；
（3）求
的取值范围．