高二年级理科数学下学期第二次月考
数学(理)
时间：120分钟 满分：150分
一、选择题：(本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的)
1、某工厂生产
三种不同型号的产品,产品数量之比依次为
.现用分层抽样方法抽出一个容量为
的样本,样本中
型号产品有
件,则此样本的容量为 （ B ）
A、40 B、
2、 设有一个直线回归方程为
,则变量x 增加一个单位时
( Ｃ )
A、 y 平均增加 1.5 个单位 B、 y 平均增加 2 个单位
C、 y 平均减少 1.5 个单位 D、 y 平均减少 2 个单位
3、 已知随机变量
的概率密度函数为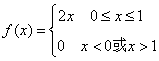
,则
( Ｄ )
A、 
B、 
C、 
D、 
4、5310被8除的余数是 （ A ）
A、1 B、
5、10个球中有一个红球，有放回的抽取，每次取出一球，直到第次才取得
次红球的概率为（ C ）
A、
B、
C、
D、
6、某博物馆要在20天内接待8所学校的学生参观，每天至多安排一所学校，其中一所人数较多的学校要连续参观3天，其余学校均只参观1天，则在这20天内不同的安排方法数是( C )
A、
B、
C、
D、
7．若
则
的值为 （ A ）
A、－1
B、
8、从6人中选出4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览，要求每个城市有一人游览，每人只游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有（B）
A、300种 B、240种 C、144种 D、96种
9、在正方体上，将任选的3个顶点连成三角形，所得三角形不是直角三角形的概率为（ A ）
A、 B、
C、
D、
10、25人排成5×5方阵，从中选出3人，要求其中任意2人不同行也不同列，则不同的选出方法种数为 ( A )
A、600
B、
11、有20张卡片分别写着数字1，2，…，19，20，将它们放入一个盒中，有4个人从中各抽取一张卡片，取到两个较小数字的二人在同一组，取得两个较大数字的二人在同一组，若其中二人分别抽到5和14，则此二人在同一组的概率等于 （D ）
A．
B．
C．
D．
12、某天下午的课程表要排入物理、化学、生物和两节自习共5节课，如果第1节不排生物，最后1节不排物理，那么不同的排课表的方法有 ( B )
A．36种 B．39 种 C．60种 D．78种
二、填空题：(本大题共4小题，每小题4分，共16分，把正确答案填写在题中的横线上)
13、已知
，则
14、若10把钥匙中只有2把能打开某锁，则从中任取2把能将该锁打开的概率为__
______.
15、在
世纪的一天，保罗与梅尔进行赌钱游戏。每人拿出
枚金币，然后玩骰子，约定谁先胜三局谁就得到
枚金币（每局均有胜负）。比赛开始后，保罗胜了一局，梅尔胜了两局，这时一件意外的事情中断了比赛，于是他们商量这枚金币应该怎样分配才合理。据此，你认为合理的分配方案是保罗和梅尔分别得到金币 3 枚和 9 枚
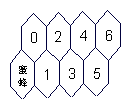
16、假定有一排蜂房，形状如图，一只蜜蜂在左下角，由于受了点伤，只
能爬，不能飞，而且只能永远向右方（包括右上，右下）爬行，从一间
蜂房爬到与之相邻的右蜂房中去，从最初位置爬到6号蜂房共有 21
种不同的爬法。
三、解答题：(本大题共6个小题，共74分。解答应写出文字说明、证明过程或演算步骤)
17、(本题满分12分)在二项式
的展开式中，若前三项的二项式系数和等于79，求展开式中系数最大的项．
解：
∴n=12
∴
设Tk+1项系数最大
则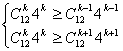
∴9.4<k<10.4
∴k=10
∴展开式中系数最大的项是
18、(本题满分12分)甲乙两人各射击一次，击中目标的概率分别是
和
，假设两人射击是否击中目标，相互之间没有影响；每人各次射击是否击中目标，相互之间也没有影响。
(1) 求甲射击4次，至少有一次没有击中目标的概率；
(2) 求甲乙两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
(3)假设某人连续2次未击中目标，则中止其射击。问：乙恰好射击5次后，被中止射击的概率是多少？
解：（1）
（2）
(3)乙第3次肯定击中，第4、第5次都没有击中，第1、第2次中至少有一次击中，
19、 (本题满分12分)从一批有5个合格品与3个次品的产品中,一件一件地抽取产品,设各个产品被抽到的可能性相同。记为直到取出的是合格品为止时所需抽取的次数,分别在下列两种情形下求出:
(1) 每次抽取的产品都不放回到这批产品中的的分布列和所需平均抽取的次数；
(2) 每次抽取的产品都立即放回到这批产品中,然后再抽取一件产品的的分布列和所需平均抽取的次数。
解： (1)第一次取出的是合格品的概率为5/8；第二次取出的是合格品（第一次取出的是次品）的概率为
；第三次取出的是合格品（第一、二次取出的是次品）的概率为
；第四次取出的是合格品（第一、二、三次取出的是次品）的概率为
。其的分布列为
|
| 1 | 2 | 3 | 4 |
| P |
|
|
|
|
所需平均抽取的次数
= 
1.5。
(2)抽查次数取1，2，3，
的整数，取出合格品的概率为5/8，取出次品的概率为3/8，前
次是次品，而第
次（
）取出正品的概率是：
（
）。其的分布列为:
|
| 1 | 2 | 3 | … |
| … |
| P |
|
|
| … |
| … |
所需平均抽取的次数= 
20、 (本题满分12分) 在袋里装30个小球，其中彩球有：n个红色、5个蓝色、10个黄色，其余为白球.
求：(Ⅰ)如果已经从中取定了5个黄球和3个蓝球，并将它们编上了不同的号码后排成一排，那么使蓝色小球互不相邻的排法有多少种？
(Ⅱ)如果从袋里取出3个都是相同颜色彩球（无白色）的概率是
，且n≥2，计算红球有几个？
(Ⅲ)根据(Ⅱ)的结论，计算从袋中任取3个小球至少有一个是红球的概率.
解：(Ⅰ)将5个黄球排成一排只有
种排法，将3个蓝球放在5个黄球所形成的6个空上，有
种放法 ,
∴所求的排法为
=5×4×3×2×6×5×4=14400（种）.
4分
(Ⅱ)取3个球的种数为
=4060,设“3个球全红色”为事件A，“3个球全蓝色”为事件B，“3个球全黄色”为事件C.
P（B）=
，
∵A、B、C为互斥事件，
∴P（A+B+C）= P（A）+P（B）+P（C）,
即
取3个球红球的个数n≤2.
又∵n≥2，故n = 2 . 8分
(Ⅲ)记“3个球中至少有一个是红球”为事件D，则
为“3个球中没有红球”,
P（D）=1－P（）=1－
或P（D）=
12分
21、（本小题满分12分）在湖南卫视的一次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并且宣布：幸运观众答对问题A可获奖金1000元，答对问题B可获奖金2000元，先答哪个题由观众自由选择，但只有第一个问题答对，才能再答第二题，否则终止答题.若你被选为幸运观众，且假设你答对问题A、B的概率分别为
、.你觉得应先回答哪个问题才能使你获得更多的奖金？请说明理由.
解：设先答A的奖金为
元，先答B的奖金为
元。则有
同理：
故知先答A ，所获的奖金期望较多
22、(本题满分14分) 从1，2，3，…，20这20个自然数中，每次任取3个数，
（1）若其和是大于10的偶数，则这样的数组有多少个？
（2）若所取三数中每两个数之间至少相隔两个自然数，则这样的数组有多少个？
解：（1）设A=
，则从中取3个数且和为偶数的取法有
种，
1，3，2； 1，3，4； 1，3，6；1，5，2； 1，5，4； 1，7，2；3，5，2
其中3个数的和不大于10的有7个。故合条件的数组共有570–7=563个。
（2）运用如下模型：将3个黑球与19个白球排成一排，且每个黑球右边各连排两个白球分别形成一个“位置”，这样只有13个白球与3个“黑白球组合”排在16个“位置”上，排法有
，对每种排法中的前20个球从左至右赋值1，2，…，20，则三个黑球上的数即为取出的数，因此所取的数组共有
个。
法二 设
,在集合B中任取三个数
作
，则
且
两两之间至少相隔两个自然数
的组合有
种不同取法，的每一种取法，对应的也有一种取法，故有
种不同的取法。