高二年级理科数学双周测试卷

　　　　　　　  　　　 鹰潭一中高二年级双周测试卷（理科）

　　　　　　　  　　　　（实验班附加题必做，其它班附加题选做）　　 命题：黄鹤飞　2008-4-15

一、选择题：（每小题5分，共60分）

1.老师为研究男女同学数学学习的差异情况，对某班50名同学（其中男同学30名，女同学20名）采取分层抽样的方法，抽取一个样本容量为10的样本进行研究，某女同学甲被抽到的概率为（　 ）

A.　B.　 C.　 D.

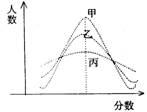
2.某次市教学质量检测，甲、乙、丙三科考试成绩的直方图如右图所示（由于人数众多，成

绩分布的直方图可视为正态分布），则由如图曲线可得下列说法中正确的一个是 （　　）

　　A．甲科总体的标准差最小　B．丙科总体的平均数最小

　　C．乙科总体的标准差及平均数都居中　 D．甲、乙、丙的总体的平均数不相同

3.设随机变量服从正态分布N(0,1),记.给出下列结论：①;②;③;④.其中正确命题的个数为（　）

A.1　　　B.2　　 C.3　　　D.4

4.若的展开式中第二项小于第一项，且不小于第三项，则的取值范围是(　　)

　　A．>－ B．≥－ 　　C．－≤≤0　D．－<≤0

5.电视台连续播放5个广告，其中3个不同的商业广告和2个不同的奥运宣传广告，要求最后播放的必须是奥运宣传广告，且2个奥运宣传广告不能连续播放，则不同的播放方式有　（　　）

A．120种　B．48种 C．36种 D．18种

6.某风景区有一个三色风车如图（红、黄、蓝每一部分各占风车所在圆的），已知风车设定的程序

是向左转或向右转（每次均转120°即停），而且逆时针方向转的概率是顺时针方向转的概率的2倍，

如图，假设红色在下边，则转三次之后蓝色在下边的概率是（　　）

　　A．　 B．　 C．　 D．

7.已知

那么的展开式中含项的系数是（　 ）

　 A.15　　B.20　　C.6　　　D.

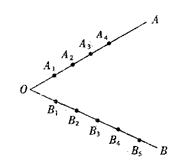
8.如图，在∠AOB的两边上分别为A₁、A₂、A₃、A₄和B₁、B₂、B₃、B₄、B₅共9个点，连结线

段A_iB_i（1≤i≤4,1≤j≤5），如果其中两条线段不相交，则称之为一对“和睦线”，则图

中共有（　　）对“和睦线”　　　　　　　

　　A．60　 B．62　 C．72 　D．124

9. 8名运动员参加男子100米的决赛. 已知运动场有从内到外编号依次为1，2，3，4，5，6，7，8的八条跑道，若指定的3名运动员所在的跑道编号必须是三个连续数字（如：4，5，6），则参加比赛的这8名运动员安排跑道的方式共有（　　）

　A．360种　　　　　B．4320种　　　　C．720种　　　　 D．2160种

10.将号码分别为1、2…9的九个小球放入一个袋中，这些小球仅号码不同，其余完全相同，甲从袋中摸出一个球，其号码为a，放回后，乙从此袋中再摸出一个球，其号码为b，则便不等式成立的事件发生的概率等于　 　　（　　）

　　A．　B．　C．　D．

11.设l为平面上过点（0，1）的直线，l的斜率等可能地取，，，0，，，，用ξ 表示坐标原点到l的距离，则随机变量ξ的数学期望Eξ=(　 )

A．　　　　  B．  C． D．　　　　　　　　　　　　　 ▲ -----------第1行

12.6个不同大小的数如图形式随机排列，设第一行的数为，第二、三行　　　 ▲　 ▲ ---------第2行

中的最大数分别为，则满足的概率是（　　 ） 　　　　 ▲　 ▲　 ▲--------第3行

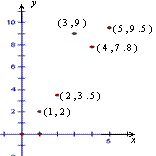　 A. 　 B.  　 C.  　　D.  

二、填空题：（每小题4分，共16分）

13. 的展开式中,的系数为　 　　 

14..五组数据的散点图如图所示，现去掉其中一组数据后，对剩下的四组数据进行线性相关分析，为使线性相关分数最大，应去掉的一组数据是 　　　　  .

15.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有　　　　

投资成功	投资失败
192次	8次

 16.某公司有5万元资金用于投资开发项目，如果成功，一年后可获利

12％；一旦失败，一年后将丧失全部资金的50%．右表是过去200例类

似项目开发的实施结果：则该公司一年后估计可获收益的期望是　　　　　 

题号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
答案

三、解答题：

17．(本小题10分)某商场经销某商品，顾客可采用一次性付款或分期付款购买．根据以往资料统计，顾客采用一次性付款的概率是0.6，经销一件该商品，若顾客采用一次性付款，商场获得利润200元；若顾客采用分期付款，商场获得利润250元．

（Ⅰ）求3位购买该商品的顾客中至少有1位采用一次性付款的概率；

（Ⅱ）求3位顾客每人购买1件该商品，商场获得利润不超过650元的概率．

18.（本小题10分）有一批数量很大的产品，其次品率是10%

　　（Ⅰ）连续所取两件产品，求两件产品均为正品的概率；

（Ⅱ）对这批产品进行抽查，每次抽出一件，如果抽出次品，则抽查终止，否则继续抽查，直到抽出次品，但抽查次数量多不超过4次，求抽查次数的分布列及期望。

19. （本小题12分）甲乙两个奥运会主办城市之间有7条网线并联，这7条网线能通过的信息量分别为l，1，2，2，2，3，3，现从中任选三条网线，设可通过的信息量为X，当可通过的信息量X≥6，则可保证信息通畅．

（1）求线路信息通畅的概率；（2）求线路可通过的信息量X的分布列；（3）求线路可通过的信息量X的数学期望．

20. （本小题12分） 已知的展开式前三项中的x的系数成等差数列。

（1）求展开式里所有的x的有理项；（2）求展开式里系数最大的项。

21．（附加题：本小题15分）甲、乙、丙三个同学一起参加某高校组织的自主招生考试，考试分笔试和面试两部分，笔试和面试均合格者将成为该高校的预录取生（可在高考中加分录取），两次考试过程相互独立．根据甲、乙、丙三个同学的平时成绩分析，甲、乙、丙三个同学能通过笔试的概率分别是0.6，0.5，0.4，能通过面试的概率分别是0.5，0.6，0.75．

（1）求甲、乙、丙三个同学中恰有一人通过笔试的概率；

（2）设经过两次考试后，能被该高校预录取的人数为，求随机变量的期望．

22. （附加题：本小题15分）设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的。现抛掷骰子根据其点数决定棋子是否移动：若投出的点数是奇数，则棋子不动；若投出的点数是偶数，棋子移动到另一顶点。若棋子的初始位置在顶点，回答下列问题。

(1)投了2次骰子，棋子才到达顶点的概率是多少？

(2)投了3次骰子，棋子恰巧在顶点的概率是多少？