高二数学教材中有关距离的问题练习
题1(第111页练习第2题)如图,已知两条异面直线所成的角为θ,在直线a、b上分别取E、F,已知A’E=m,AF=n,EF=l,求公垂线A A′的长d.
解:![]() ,
,
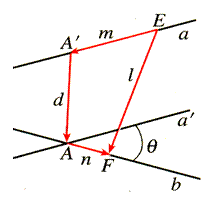
![]()
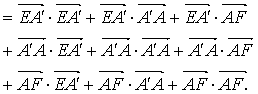
∵ ![]() ,
,
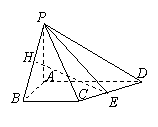
<![]() >=π—θ(或θ),
>=π—θ(或θ),
∴![]()
![]() ,
,
当E,F在公垂线同一侧时取负号
当d等于0是即为“余弦定理”
∴ ![]() .
.
 变式1
变式1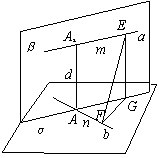 .已知:两条异面直线a、b所成的角为θ,它们的公垂线段AA1的长度为d,在直线a、b上分别取点E、F,设A1E=m,AF=n,求证:EF=(92(26))
.已知:两条异面直线a、b所成的角为θ,它们的公垂线段AA1的长度为d,在直线a、b上分别取点E、F,设A1E=m,AF=n,求证:EF=(92(26))
证明:设经过b与a平行的平面为α,经过a和AA1的平面为β,
α∩β=c,则c∥a,因而b,c所成的角等于θ,且AA1⊥c,
又∵AA1⊥bÞAA1⊥α,由两个平面垂直的性质定理有
EG⊥α.连结FG,则EG⊥FG,在Rt△EFG中,EF2=EG2+FG2
∵AG=m,∴在△AFG中,FG2=m2+n2-2mncosθ
∵EG=d,∴EF2=d2+m2+n2-2mncosθ
如果点F(或E)在点A(或A1)的另一侧,则
EF2=d2+m2+n2+2mncosθ
因此EF=.
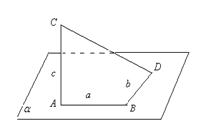
变式2:(P92练习第3题)如图,线段AB,BD在平面内,BD⊥AB,线段AC⊥α,且AB=a,BD=b,AC=c,求C,D间的距离.
![]() .
.
变式3:
(P106例2):如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处。从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为![]() 和
和![]() ,CD的长为
,CD的长为![]() , AB的长为
, AB的长为![]() 。求库底与水坝所成二面角的余弦值。
。求库底与水坝所成二面角的余弦值。
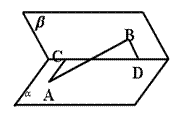 解:如图,
解:如图,![]()
![]()
![]()
![]()
![]()
![]()
于是,得![]()
设向量 ![]() 与
与![]() 的夹角为
的夹角为![]() , 就是库底与水坝所成的二面角。
, 就是库底与水坝所成的二面角。
因此, ![]()
库底与水坝所成二面角的余弦值为![]()
 变式4: (P107练习第2题)已知在一个
变式4: (P107练习第2题)已知在一个![]() 的二面角的棱长有两点
的二面角的棱长有两点![]() ,
,![]() 分别是在这个二面角的两个平面内,且垂直于线段
分别是在这个二面角的两个平面内,且垂直于线段![]() ,又知
,又知![]() ,求
,求![]() 的长
的长![]()
解:由已知![]()
![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
![]() .
.
变式5:(P113习题![]() 的棱长为1,点M是棱
的棱长为1,点M是棱![]() 的中点,点O是
的中点,点O是![]() 的中点,求证:OM是异面直线
的中点,求证:OM是异面直线![]() 与
与![]() 的公垂线,并求OM的长.
的公垂线,并求OM的长.
解: 以A为原点建立坐标系,得下列坐标:
![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
![]() .
.
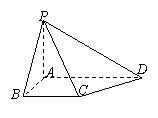
题2 (P119复习参考题B组第3题)如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和AC,侧棱SA⊥底面ABCD,且SA=AB=BC=1,AD=0.5.
(1)四棱锥S-ABCD的体积;
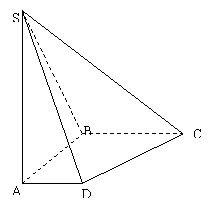 (2)求面SCD与面SAB所成二面角的大小.
(2)求面SCD与面SAB所成二面角的大小.
解:(1)直角梯形ABCD的面积为
![]() 。
。
∴四棱锥S-ABCD的体积为
![]() .
.
(2)建立如图空间直角坐标系Axyz,则
![]() ,
,
![]() .
.
∵SA⊥平面ABCD,AD⊥AB, ∴向量![]() 是面SAB的一个法向量.
是面SAB的一个法向量.
设平面SCD的一个法向量为![]() ,由
,由
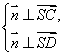
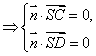
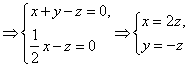
令![]() ,则
,则![]() .
.
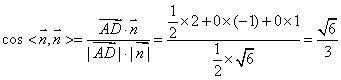 .
.
∴面SCD与面SAB所成二面角的大小![]() .
.
变式1:如图,在底面是直角梯形的四棱锥S-ABCD中, ![]() ,
,![]()
![]()
(1)求证:面SAB⊥面SBC;
(2)E点是SC的中点,求证:DE⊥面SBC.
 变式2:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB=a,AD=
变式2:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB=a,AD=
⑴二面角P-CD-A的大小(用反三角函数表示);
⑵点A到平面PBC的距离.
解:如图,在平面ABCD内,过点A作AE⊥CD,垂足为E,连结PE,
有PA⊥平面ABCD,由三垂线定理知PE⊥CD,
故∠PEA是二面角P-CD-A的平面角
在Rt△DAE中,AD=
则AE=ADsin∠ADC=a
在Rt△PAE中,tan∠PEA=
故二面角P-CD-A的大小为arctan
⑵在平面PAB中,过点A作AH⊥PB,垂足为H,有PA⊥平面ABCD,AB⊥BC,PA⊥BC,则有BC⊥平面PAB.
又AH∩平面PAB,因此BC⊥AH.又AH⊥PB,故AH⊥平面PBC.
因此线段AH的长即为点A到平面PBC的距离.
在等腰直角△PAB中,AH=a,即点A到平面PBC的距离为a.
 题3(P114习题3.2B组第3题)如图,在棱长为
题3(P114习题3.2B组第3题)如图,在棱长为![]() 的正方体
的正方体![]() 中,点E,F分别是棱AB,BC上的动点,且AE=BF.
中,点E,F分别是棱AB,BC上的动点,且AE=BF.
(1)求证![]() ;
;
(2)当三棱锥![]() 的体积取得最大时,求二面角
的体积取得最大时,求二面角![]() 的正切值.
的正切值.
解:(1)以C为坐标原点,以CO、CB、![]() 为x、y、z轴建立空间直角坐标系C-xyz,设
为x、y、z轴建立空间直角坐标系C-xyz,设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,即
,即![]() .
.
(2) ![]()
当且仅当![]() 时,即E,F分别为AB,BC中点时,
时,即E,F分别为AB,BC中点时, ![]() 最大.
最大.
取EF的中点G,连结BG, ![]() ,则
,则![]() ,BG⊥EF,
,BG⊥EF, ![]() ⊥EF,即
⊥EF,即![]() 是二面角
是二面角![]() 的平面角.
的平面角.
又![]() ,
,
∴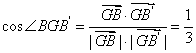 .
.
即![]() .
.
 ∴二面角
∴二面角![]() 的正切值是
的正切值是![]() .
.
题4:(P114习题3.2B组第2题)在如图的实验装置中,正方形框架的边长都是1, 且平面ABCD与平面互相垂直.活动弹子M, N分别在正方形的对角线AC和BF上移动,且CM和BN若的长度相等,记CM=BN=a(0<a<).
(1)求MN的长;
(2)当a为何值时,MN的长最小;
(3)当MN长最小时,求面MNA与面MNB所成的二面角α的余弦值。
解:以B为坐标原点,以BA、BE、BC为x、y、z轴建立空间直角坐标系,则
![]() ,
,
(1)∵![]() ,
,
∴![]() .
.
(2) ∵![]() ,
,
∴当![]() 时,
时, ![]() .
.
(3)由(2)知当M, N分别为AC、BF中点时MN的长最小,则
![]() .
.
取MN的中点G,连结AG, BG,则![]() .
.
∵AM=AN,BM=BN, G为MN中点,
∴AG⊥MN,BG⊥MN,即∠AGB即为二面角α的平面角.
∵![]() ,
,
![]() .
.
 所求二面角α的余弦值为
所求二面角α的余弦值为![]() .
.
 变式:如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<)(2002年全国(18)、天津(18乙))
变式:如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<)(2002年全国(18)、天津(18乙))
1.求MN的长;
2.当a为何值时,MN的长最小;
3.当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
本小题主要考查线面关系、二面角和函数极值等基础知识,考查空间想象能力和推理论证能力.
解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连接PQ,依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形.
∴MN=PQ,
由已知,CM=BN=a,CB=AB=BE=1,
AC=BF=.
∴,即CP=BQ=.
MN=PQ=(0<a<)
∴MN=(0<a<)
(2)由(1)MN=
所以,当a=时,MNmin=
即当M、N分别移动到AC、BF的中点时,MN的长度最小,最小值为
(3)取MN的中点G,连接AG、BG,
∵AM=AN,BM=BN,∴AG⊥MN,BG⊥MN,∴∠AGB即为二面角α的平面角。
又AG=BG=,所以由余弦定理有
cosα=.故所求二面角α=arccos(-).
题5:(P114习题3.2B组第1题)如图,四面体DABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点;异面直线AD与BE所成角为![]() ,且
,且![]() ,求四面体DABC的体积.
,求四面体DABC的体积.
解:以B为坐标原点,以BC、BA、BD为x、y、z轴建立空间直角坐标系Bxyz,则
![]() ,
,
设![]()
![]() .
.
![]() .
.
∴![]() .
.
题6:(P112习题
(1)计算DE的长;
(2)求点O到平面ABC的距离.
解:(1) ![]()
![]()
![]()
![]() ,
,![]() .
.
(2) ![]()
![]()
 .
.
点O到平面ABC的距离是![]() .
.
题7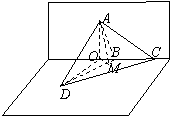
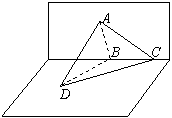 如图,设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠CBA=∠DBC=120°,求:(91上海)
如图,设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠CBA=∠DBC=120°,求:(91上海)
⑴AD的连线与平面BCD所成的角;
⑵AD得连线与直线BC所成的角;
⑶二面角A-BD-C的大小
解:⑴过A在平面ABC内作AO⊥BC于O,连接DO,
∵ 面ABC⊥面BCD,∴ AO⊥面BCD,
于是∠ADO就是所求AD与平面BCD所成的角,且∠AOD=90°.
设AB=BC=BD=2,则AO=DO=,△AOD为等腰直角三角形,
∠ADO=45°.
⑵注意到BC⊥AO,BC⊥DO,∴ BC⊥面AOD.
∴ BC⊥AD,即BC与AD所成交为90°
⑶在平面BCD内作OM⊥BD于M,连接AM
∵ AO⊥面BCD,由三垂线定理知:AM⊥BD
∴∠AMO即为二面角A-BD-C的平面角的补角,
计算可得:OM=,又∠AOM=90°,AO=
∴∠AMO=arctan2.
于是二面角A-BD-C的大小为π-arctan2.