08年春季高二年级数学半期质量检测
数学试卷(理科)
第一卷
（时间 120分钟，满分150分，命题人：马杰 ，审题人：许志兴）
一 选择题（每小题5分，共60分）
1． 垂直于同一平面的两条直线的位置关系是 （ ）
A．相交 B．异面 C．平行 D．都有可能
2．在下列条件中，可判断平面α与β平行的是 （ ）
A．α、β都垂直于平面r.
B．α内存在不共线的三点到β的距离相等.
C．l，m是α内两条直线，且l∥β，m∥β.
D．l，m是两条异面直线，且l∥α，m∥α, l∥β，m∥β.
３．一条直线与平面a成60°角，则这条直线与平面内的直线所成角的取值范围是 （ ）
A［0°，90°］ B
C［60°，180°］ D［60°，90°］
４．球面上A、B两点的球面距离是
，过这两点的半径的夹角是60°，则这个球的体积为 （ ）
A．48 B． C．24 D．18
5．图中给出的是长方体形木料想象沿图中平面所示位置截长方体，若那么截面图形是下面四个图形中的 ( )
A B C
D
６.已知平面α∥平面β，它们之间的距离为d，直线a
α，则在β内与直线a相距为2d的直线有
（ ）
Ａ．一条 Ｂ．无数条 Ｃ．两条 Ｄ．不存在
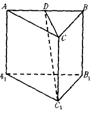7. 正三棱柱ABC—A1B1C中，D是AB的中点，CD等于
，则顶点A1到平面CDC1的距离为 （ ）
A．
B．1 C．
D．
8.侧棱长为2a的正三棱锥其底面周长为9a，则棱锥的高为 （ ）
A.a B. 2a C.
D.
9．已知AB是异面直线a、b的公垂线段，AB=2，且a与b成30°角，在直线a上取AP=4，则点P到直线b的距离为 （ ）
A.
B.4 C.2
D.或2
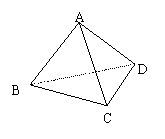10．四面体A—BCD中，
，其余棱长均为1，则二面角
A—BC—D的大小是 （ ）
A.
B.
C.
D.
11.已知a、b是两条所成角为60
的异面直线。过其公垂线上一点作与这两条直线均为60角的直线有几条
（ ）
A. 1条 B. 2条 C.3条 D. 4条
12.一个正四棱锥与一个正四面体的所有棱长都为a,把正四棱锥的一个侧面和正四面体的一个面重合后，得到的多面体是 （ ）
A.五面体 B.六面体 C.七面体 D.八面体
二 填空题（每小题4分，共16分）
13.三个平面至多把空间分成 ___________个部分.
14.已知集合A=｛1，2，3，4，5｝集合B=｛a,b,c,d,e,f｝则从集合A到集合B能构成_______________个函数
15一个正四面体的内切球与各个顶点的外接球的表面积之比为________.
16.已知点P，直线
，给出下列命题：
①若
②若
③若
④若
⑤若
其中正确命题的序号是__________________(把所有正确命题的序号都填上).
简阳中学2008年春季09高年级半期质量检测
数学试卷(理科) 答题卷
一 选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二 填空题
13._____________14 .______________15._____________16______________
三 解答题
17. （12分）已知空间三点A（-2，0，2），B（-1，1，2），C（-3，0，4），设
= a,
= b , （1）求a、b的夹角
；
（2）若向量ka + b 与向量ka – 2b 互相垂直，求k的值
18.（12分）如图，正方体ABCD-A1B1C1D1的边长为a，E、F
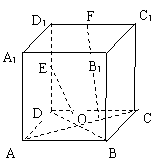分别是DD1与D1C1的中点O是AC与BD的交点，
（1） 求直线EO与BF的夹角
（2） 求直线EO与BF的距离
19（12分）.如图，正三角形ABC的边长为2，AC、BC
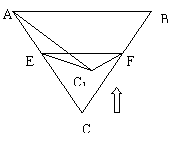的中点分别是E、F， 沿着EF折成一个直二面角后.
（1）.求AC1的长度。
(2 ) .求AC1与平面EFC1所成角的大小。
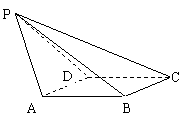
20.（12分）已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，
底面ABCD，且PA=AD=DC=AB=1，M是PB的中点。
（1）证明：面PAD⊥面PCD；
（2）求二面角A－MC－B的大小。
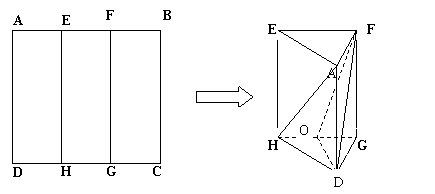
21（12分）如图所示，正方形的边长为3，E、F、G、H是分别正方形边AB 、CD的三等分点，将正方形沿EH、FG对折成一个三棱柱AEF-DHG，O是HG的中点。（1）求证：AH∥平面ODF （2）求点A到平面ODF的距离。
 |
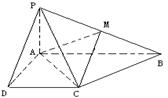
22.已知四棱锥P-ABCD,PB⊥AD,侧面PAD为边长等于2的正三角形。底面ABCD为菱形。
侧面PAD与底面ABCD所成的二面角为1200
(1) 求点P到平面ABCD的距离。
(2) 求异面直线PA与BD所成的角的大小。
(3) 求面APB与面CPB所成二面角的大小。