高二数学同步检测一
平面与空间直线
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.
第Ⅰ卷(选择题)
一、选择题(本大题共10小题,在每小题给出的四个选项中,选择一个符合题目要求的选项)1.列命题是真命题的是( )
A.空间不同三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.四边形确定一个平面
D.和同一直线都相交的三条平行线在同一平面内
答案:D
解析:根据公理3(经过不在同一条直线上的三点,有且只有一个平面)知不在同一直线上的三点,才能确定一个平面,所以A错.
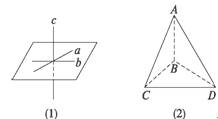
如图(1),a,b,c三条直线两两相交,但a,b,c不共面,所以B错误.
如图(2),显然四边形ABCD不能确定一个平面.
2.已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于( )
A.30° B.30°或150°
C.150° D.以上结论都不对
答案:B
解析:由等角定理可知∠PQR与∠ABC相等或互补,即∠PQR=30°或150°.
3.如右图,α∩β=l,A∈β,B∈β,AB∩l=D,C∈α,则平面ABC和平面α的交线是( )
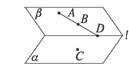
A.直线AC B.直线BC
C.直线AB D.直线CD
答案:D
解析: 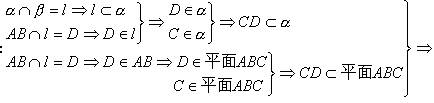
CD为平面ABC与平面α的交线.故选D.
4.如图,点P,Q,R,S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的图是( )
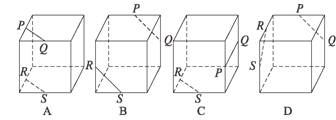
答案:C
解析:A,B中的PQ与RS相互平行;D中的PQ与RS相交;由两条直线异面的判定定理可知C中的PQ与RS异面.
5.对“a,b是异面直线”的叙述,正确的是( )
①a∩b=![]() 且a不平行于b
②a
且a不平行于b
②a![]() 平面α,b
平面α,b![]() 平面β且α∩β=
平面β且α∩β=![]() ③a
③a![]() 平面α,b
平面α,b![]() 平面α ④不存在平面α,使a
平面α ④不存在平面α,使a![]() 平面α且b
平面α且b![]() 平面α成立
平面α成立
A.①② B.①③ C.①④ D.③④
答案:C
解析:根据“异面直线是不同在任何一个平面内的两条直线”的定义知,结论④正确.空间不相交的两条直线除平行外就是异面,故对于结论①,既然两直线不平行,则必然异面.分别在两个平面内的两条直线可能平行,故②不正确.平面内的一条直线和平面外的一条直线除异面外还可能平行或相交,故③不正确.综上所述,只有①④正确.
6.右图是一个无盖的正方体盒子展开后的平面图,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的值为…( )
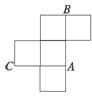
A.180° B.90° C.60° D.45°
答案:C
解析:把平面图形还原为立体图形,找准A、B、C三点相对位置,可知∠ABC在等边△ABC内.
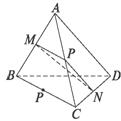
7.在空间四边形ABCD中,M,N分别是AB,CD的中点,设BC+AD=2a,则MN与a的大小关系是( )
A.MN>a B.MN=a C.MN<a D.不能确定
答案:C
解析:如图,取AC中点P,则MP![]()
![]() BC,NP
BC,NP![]() AD,且MP+NP=
AD,且MP+NP=![]() (BC+AD)=a>MN,故C正确.
(BC+AD)=a>MN,故C正确.
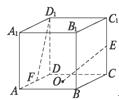
8.如图,在棱长为1的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案:B
解析一:如图(1),取面CC1D1D的中心为H,连结FH、D1H.易知OE∥FH,所以∠D1FH为所求异面直线所成的角.在△FHD1中,
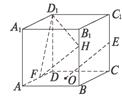
FD1=![]() ,FH=
,FH=![]() ,D1H=
,D1H=![]() 由余弦定理,得∠D1FH的余弦值为
由余弦定理,得∠D1FH的余弦值为![]() .
.
解析二:如图(2),取BC中点为G.连结GC1、FD1,则GC1∥FD1.再取GC中点为H,连结HE、OH,则∠OEH为异面直线所成的角.
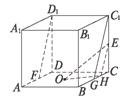
在△OEH中,OE=![]() ,HE=
,HE=![]() ,OH=
,OH=![]() .
.
由余弦定理,可得cos∠OEH=![]() .
.
9.空间有四点A,B,C,D,每两点的连线长都是2,动点P在线段AB上,动点Q在线段CD上,则P,Q两点之间的最小距离为( )
A.1
B.![]() C.
C.![]() D.
D.![]()
答案:C
解析:PQ的最小值应是AB,CD的公垂线段长.易知P,Q分别是AB,CD中点时,PQ⊥AB,PQ⊥CD.在Rt△BQP中,
∵BQ=![]() ,BP=1,∴PQ=
,BP=1,∴PQ=![]() =
=![]() .
.
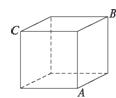
10.右图是正方体的平面展开图,则在这个正方体中:
①BM与ED平行;②CN与BE是异面直线;③CN与BM成60°角;④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
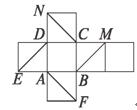
A.①②③ B.②④ C.③④ D.②③④
答案:C
解析:将上面的展开图还原成如图所示正方体.容易知道BM与ED异面,CN与BE平行,故①②不正确.
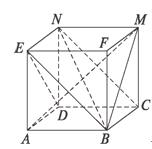
因为BE∥CN,所以CN与BM所成的角是∠EBM=60°,延长CD至D′,使DD′=DC,
则D′N∥DM,∠BND′就是DM与BN所成的角.设正方体的棱长为1,
因为BN=![]() a,ND′=
a,ND′=![]() a,BD′=
a,BD′=![]() a,所以BN2+D′N2=D′B2,即BN⊥ND′,BN⊥DM.
a,所以BN2+D′N2=D′B2,即BN⊥ND′,BN⊥DM.
第Ⅱ卷(非选择题)
二、填空题(本大题共4小题,答案需填在题中横线上)
11.以下四个命题:
①A∈l,A∈α,B∈l,B∈α![]() l
l![]() α;
α;
②A∈α,A∈β,B∈α,B∈β![]() α∩β=AB;
α∩β=AB;
③l![]() α,A∈l
α,A∈l![]() A
A![]() a;
a;
④A,B,C∈α,A,B,C∈β,且A,B,C不共线![]() α与β重合.
α与β重合.
其中推理正确的序号是__________.
答案:①②④
解析:由公理1知①正确;由公理2知②正确;由公理3知④正确;而③中直线l可能与平面α相交于A.故③不正确.
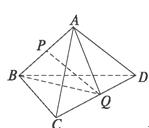
12.空间四条直线,两两相交可确定平面的个数最多有____________个.
答案:6
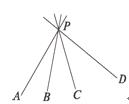
解析:显然,任两条相交直线若都能确定一个平面(不重复),此时平面个数最多.如图,平面PAB,平面PAC,平面PAD,平面PBC,平面PCD,平面PBD,共6个.
13.(2006全国重点中学一模,11)给出三个命题:
①若两条直线和第三条直线所成的角相等,则这两条直线互相平行;
②若两条直线都与第三条直线垂直,则这两条直线互相平行;
③若两条直线都与第三条直线平行,则这两条直线互相平行.
其中不正确的序号是__________.
答案:①②
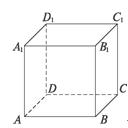
解析:在如图所示的正方体ABCD—A1B1C1D1中,A1D1⊥D1D,C1D1⊥D1D,
即A1D1与D1D,C1D1与D1D所成的角都是90°,但A1D1与C1D1不平行,可知①②不正确,由公理4可知③正确.
14.在正方体ABCD—A1B1C1D1中,如果E、F分别为AB、CC1的中点,那么异面直线A1C与EF所成的角等于_______________.
答案:arccos![]()
解析:延长AA1到P,使A1P=![]() AA1,
AA1,
连结PF,则PF∥A1C,设A1A=a.
则PE2=(![]() a)2+(
a)2+(![]() a)2=
a)2=![]() a2,
a2,
EF2=(![]() a)2+a2+(
a)2+a2+(![]() a)2=
a)2=![]() a2,PF2=A1C2=3a2.
a2,PF2=A1C2=3a2.
∴cos∠PEF=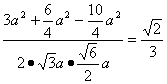 .
.
∴直线A1C与EF所成的角等于arccos![]() .
.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
15.已知正方体ABCD—A1B1C1D1中,E、F分别是D1C1、B1C1的中点,AC∩BD=P,A1C1∩EF=Q,求证:
(1)D、B、F、E四点共面;
(2)若直线A1C交平面DBFE于点R,则P、Q、R三点共线.
(1)证法一:∵EF是△D1B1C1的中位线,
∴EF∥B1D1.
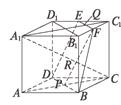
在正方体AC1中,B1D1∥BD,
∴EF∥BD.
由公理3知EF、BD确定一个平面,
即D、B、F、E四点共面.
证法二:延长BF,CC1交于点G,延长DE,CC1交于点G′.
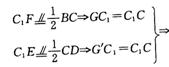 G与G′重合DE,BF是相交直线
G与G′重合DE,BF是相交直线![]() D,B,F,E四点共面.
D,B,F,E四点共面.
(2)证明:正方体ABCD—A1B1C1D1中,设A1ACC1确定的平面为α,设平面DBFE为β,
∵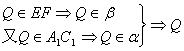 为α、β的公共点.
为α、β的公共点.
同理,P亦为α、β的公共点,
∴ R∈PQ,即P、Q、R三点共线.
R∈PQ,即P、Q、R三点共线.
点评:证明多点共线,可先由两点确定一直线,证其余点在直线上.要证点在一条直线上,只需证明这点是两平面的公共点,而直线是两个平面的交线,这是证点在直线上的常用方法.
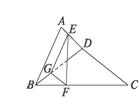
16.如图,E、F、G、H分别是空间四边形ABCD各边上的点,且有AE∶EB=AH∶HD=m,CF∶FB=CG∶GD=n.
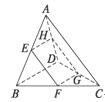
(1)证明E、F、G、H四点共面.
(2)m、n满足什么条件时,EFGH是平行四边形?
(3)在(2)的条件下,若AC⊥BD,试证明EG=FH.
(1)证明:
∵AE∶EB=AH∶HD,∴EH∥BD.
∵CF∶FB=CG∶GD,
∴FG∥BD.∴EH∥FG.∴E、F、G、H四点共面.
(2)解:当且仅当EH![]() FG时,四边形EFGH为平行四边形.
FG时,四边形EFGH为平行四边形.
∵![]() ,∴EH=
,∴EH=![]() BD.
BD.
同理,FG=![]() BD.由EH=FG得m=n.
BD.由EH=FG得m=n.
故当m=n时,四边形EFGH为平行四边形.
(3)证明:当m=n时,AE∶EB=CF∶FB,∴EF∥AC.
又∵AC⊥BD,∴∠FEH是AC与BD所成的角.∴∠FEH=90°.
从而EFGH为矩形,∴EG=FH.
点评:空间四边形是立体几何的一个基本图形,它各边中点的连线构成平行四边形;当两对角线相等时该平行四边形为菱形;当两对角线互相垂直时,该平行四边形为矩形;当两对角线相等且互相垂直时,该平行四边形为正方形.
17.如图,a,b,c为不共面的三条直线,且相交于一点O,点M,N,P分别在直线a,b,c上,点Q是b上异于N的点,判断MN与PQ的位置关系,并予以证明.
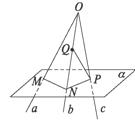
证法一:(反证法)
假设MN与PQ共面于β,则点M,N,P,Q∈β.
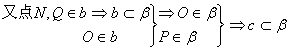
同理,a![]() β.
β.
∴a,b,c共面,与已知a,b,c不共面矛盾.故MN与PQ为异面直线.
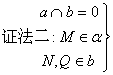
![]()

点Q![]() MN,
MN,
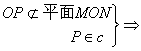 点P
点P![]() 平面MON.
平面MON.
故平面MON内一点Q与平面外一点P的连线PQ与平面内不过Q点的直线MN是异面直线.
18.如图所示,今有一正方体木料ABCD—A1B1C1D1,其中M,N分别是AB,CB的中点,要过D1,M,N三点将木料锯开,请你帮助木工师傅想办法,怎样画线才能顺利完成?
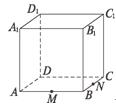
解:作法如下:
(1)连结MN并延长交DC的延长线于F,连结D1F交CC1于Q,连结QN;
(2)延长NM交DA的延长线于E,连结D1E交A1A于P,连结MP;
(3)依次在正方体各个面上画线D1P,PM,MN,NQ,QD1,即为木工师傅所要画的线.
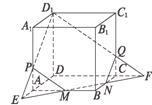
19.如图,AB,CD是两条异面直线,AB=CD=3a,E,F分别是线段AD,BC上的点,且ED=2AE,FC=2BF,EF=![]() a,G∈BD,EG∥AB.
a,G∈BD,EG∥AB.
(1)求AB与CD所成的角;
(2)求△EFG的面积.
解:(1)∵ED=2AE,EG∥AB,∴DG=2BG.
∵FC=2BF,∴FG∥DC.
∴∠EGF即为AB与CD所成的角或其补角.
∵AB=CD=3a,EG=2a,GF=a,又EF=![]() a,
a,
∴cos∠EGF=![]() .
.
∴∠EGF=120°.∴AB与CD所成的角为60°.
(2)S△EFG=![]() EG·GF·sin120°
EG·GF·sin120°
=![]() ×2a×a×sin120°
×2a×a×sin120°
=![]() a2.
a2.