（7）曲线方程和圆
一、选择题（本大题共10小题，每小题5分，共50分）
1．已知以方程F(x，y)=0的解为坐标的点都在曲线C上，则下列说法正确的有
（ ）
A．方程F(x，y)=0的曲线是C
B．曲线C的方程是F(x，y)=0
C．不在曲线C上的点的坐标不是方程F (x，y)=0的解
D．曲线C上的点的坐标都是方程F(x，y)=0的解
2．方程x+
=0所表示的图形是 （ ）
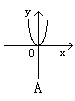
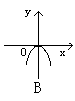
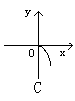
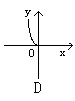
3．到点A（-1，0）和点B（1，0）的斜率之积为-1的动点P的轨迹方程是 （ ）
A．x2+y2=1 B． x2+y2=1 (x≠±1)
C．x2+y2=1 (x≠0) D．y=
4．若直线y=kx+2和曲线2x2+3y2=6有两个公共点，则k的值是 （ ）
A．k=±
B． k≠±
C．-<k< D．k>或k<-
5．在圆(x-2)2+(y+3)2=2上与点（0，-5）距离最大的点的坐标是
A．(5，1) B．（4，1）
C．（
+2，-3） D．（3，-2）
6．方程x2+y2+ax+2ay+
A．a<-2 B．-
<a<
7．过点M（3，2）作⊙O：x2+y2+4x-2y+4=0的切线方程是 （ ）
A．y=2 B．5x-12y+9=0
C．12x-5y-26=0 D．y =2或5x-12y+9=0
8．圆x2+y2-4x+4y+6=0截直线x-y-5=0所得的弦长为 （ ）
A． 
B． 
C．1 D．5
9．已知一个圆的方程为 
(θ为参数)，则该圆和直线x-y+2=0的交点的个数
是 （ ）
A．1 B．
10．两圆x2+y2-2x=0与x2+y2+4y=0的位置关系是 （ ）
A．相离 B．外切 C．相交 D．内切
二、填空题（本大题共4小题，每小题6分，共24分）
11．曲线y=x与圆 x2+y2=4所围成的最小区域的面积是 ．
12．设圆x2+y2-4x-5=0的弦AB的中点为P（3，1），则直线AB的方程是 ．
13．圆心在直线y=x上且与x轴相切于点（1，0）的圆的方程是 ．
14．集合A={(x，y) x2+y2=4}，B={(x，y)( x-3)2+(y-4)2=r2}，其中r>0，若A∩B中有且仅有一个元素，则r的值是 ．
三、解答题（本大题共6小题，共76分）
15．已知点A(0，2)和圆C：
，一条光线从A点出发射到x轴上后沿圆的切线方向反射，求这条光线从A点到切点所经过的路程．（12分）
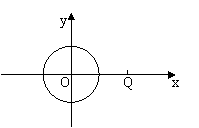
16． 如图，已知直角坐标平面上点Q（2，0）和圆C：x2+y2=1，动点M到圆C的切线长与MQ的比等于．求动点M的轨迹方程，并说明它表示什么曲线．（12分）
17．已知圆C和y轴相切，圆心C在直线
上,且被直线y=x截得的弦长为
，求圆C的方程．（12分）
18．已知实数
满足方程
的最大值与最小值． （12分）
19．已知
为参数，圆C：
（1）指出圆C的圆心和半径；（2）求出圆心C的轨迹方程． （14分）
20．已知圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3：1；
③圆心到直线l：x-2y=0的距离为
，求该圆的方程．（14分）
参考答案
一．选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | B | D | D | D | D | A | B | C |
二．填空题（本大题共4小题，每小题6分，共24分）
11．π 12．x + y -4=0 13．(x -1)2+( y -1)2=1 14． 3或7
三、解答题（本大题共6题，共76分）
15．（12分）
[解析]：设反射光线与圆相切于D点．点A关于x轴的对称点的坐标为A１(０，－２)，则光从A点到切点所走的路程为｜Ａ１Ｄ｜．
在Ｒｔ△Ａ１ＣD中，
∴｜Ａ１Ｄ｜＝
．
即光线从A点到切点所经过的路程是
．
16．（12分）
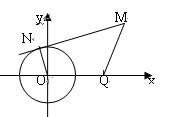
[解析]：如图，设直线MN切圆于N，则动点M组成的集合是：P={M MN=MQ}．
因为圆的半径ON=1，所以MN2=MO2-ON2=MO2-1．
设点M的坐标为（x，y），
则
整理得
它表示圆，该圆圆心的坐标为（4，0），半径为
17．（12分）
[解析]：设圆心坐标为（
所以圆心到直线y =x的距离为
由半径、弦心距、半径的关系得
所求圆的方程为
18．（12分）
[解析]：设
，
则
=
设
（
），则
，
所以，
．
19．（14分）
[解析]：（1）将圆C方程配方得：
所以圆心C的坐标为（
），半径为a
（2）设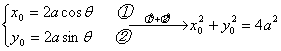
所以圆心C的轨迹方程为
20．（14分）
[解析]：（法一）设圆P的圆心为P（a，b），半径为r，则点P到x轴，y轴的距离分别为b，a．由题意可知圆P截x轴所得劣弧对的圆心角为90°，圆P截x轴所得的弦长为
，2b=，得r2=2b2，又圆P被y轴所截得的弦长为2，由勾股定理得r2=a2+1，得2b2- a2=1．
又因为P（a，b）到直线x -2y=0的距离为
，得d=
，即有
综前述得
，
解得
，
，于是r2= 2b2=2
所求圆的方程是
，或
（法二）设圆的方程为
，
令x =0，得
，
所以
，得
再令y=0，可得
，
所以
，得
，
即
，从而有2b2- a2=1．
又因为P（a，b）到直线x -2y=0的距离为
，得d=
，即有
综前述得，解得
，
，于是r2= 2b2=2
所求圆的方程是
，或