高二级数学椭圆测试及答案

（9）椭圆

一、选择题（本大题共10小题，每小题5分，共50分）

1．如果方程x ²+ky ²=2表示焦点在y轴上的椭圆，那么实数k的取值范围是　　　　　 （　　）

　　　 A．(0, +∞)　　　　　　　B．(0, 2)　　　　　　　　　C．(1, +∞) 　　　　　　D．(0, 1)

2．直线y = x +1被椭圆x ²+2y ²=4所截得的弦的中点坐标是　　　　　　　　　　　　　　　　　　（　　）

　　　 A．(, -)　　　　　　B．．(-, ) 　　　 C．(, -)　　　　　　D．(-, ) 　

3．平面内有两定点A、B及动点P，设命题甲是：“PA+PB是定值”，命题乙是：“点P的轨迹是以A．B为焦点的椭圆”，那么　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．甲是乙成立的充分不必要条件　　　　　　　B．甲是乙成立的必要不充分条件

C．甲是乙成立的充要条件　　　　　　　　　　　　D．甲是乙成立的非充分非必要条件

4．若椭圆的焦距长等于它的短轴长，则椭圆的离心率等于　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 　　　　　　　　　　B． 　　　　　　　　　C．　　　　　　　　　 D．2

5．椭圆的中心到准线的距离是　　　　　　　　　　　　　　　　　　　　　　 　　 　　　　 （　　）

A．2　　　　　　　　　　　　B．3　　　　　　　　　　　　C．　　　　　　　　　　D．

6．椭圆的焦点为F₁和F₂，点P在椭圆上，如果线段P F₁的中点在y轴上，那么P F₁是PF₂的　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．7倍　　　　　　　　　　B．5倍　　　　　　　　　　C．4倍　　　　　　　　　　D．3倍

7．椭圆4 x ²+y ²=k两点间最大距离是8，那么k=　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．32　　　　　　　　　　　B．16　　　　　　　　　　　 C．8　　　　　　　　　　 　D．4

8．中心在原点，准线方程为x =±4，离心率为的椭圆方程是　　　　　　　　　　　　　　 （　　）

A． 　　　 B． 　　　 C． + y ²=1　　　　 D． x ²+=1

9．直线与椭圆恒有公共点，则b的取值范围是（　　）

　　　 A．（0，1）　　　　　　B．（0，5）　　　　　　C．　 D．

10．若椭圆的对称轴在坐标轴上，短轴的一个端点与两个焦点组成一个正三角形，焦点到椭圆上点的最短是距离为，这个椭圆方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　B．　　　　

　　　 C．　　　　　　　　　　　　　　　　　　 D．以上都不对

二、填空题（本大题共4小题，每小题6分，共24分）

11．椭圆x ²+4y ²=1的离心率是　　　　　　　　　　 ．

12．设椭圆（a>b>0）的右焦点为F₁，右准线为l₁，若过F₁且垂直于x轴的弦的长等于点F₁到l₁的距离，则椭圆的离心率是　　　　　　　　  ．

13．一个椭圆的离心率为e=0.5，准线方程为x=4，对应的焦点F（2，0），则椭圆的方程为　　　　　　　　　　　　　　　　 ．

14．椭圆的焦点为F₁、F₂，点P为其上的动点．当∠F₁PF₂为钝角时，点P的横坐标的取值范围是　　　　　　　　　　　　　　  ．

三、解答题（本大题共6小题，共76分）

15．求椭圆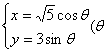为参数）的准线方程．（12分）

16．求经过点P（1，1），以y轴为准线，离心率为的椭圆的中心的轨迹方程．（12分）

17．若直线y=x+t与椭圆 相交于A、B两点，当t变化时，求AB的最大值．(12分)

18．已知椭圆的中心在原点O，焦点在坐标轴上，直线y = x +1与该椭圆相交于P和Q，且OP⊥OQ，PQ=，求椭圆的方程．（12分）

19．设椭圆的中心是坐标原点，长轴在x轴上，离心率e=，已知点P（0，）到这个椭圆上的点的最远距离是，求这个椭圆的方程，并求椭圆上到点P的距离等于的点的坐标．（14分）

20．设椭圆方程为，过原点且倾斜角为的两条直线分别交椭圆于A、C和B、D两点．（1）用表示四边形ABCD的面积S；（2）当时，求S的最大值．（14分）

参考答案

一．选择题（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	B	B	C	B	A	B	A	C	A

二．填空题（本大题共4小题，每小题6分，共24分）

11．e= 　　12． 　　 13．3 x ²+4 y ²-8 x =0　　14．-< x <

三、解答题（本大题共6题，共76分）

15．（12分）

[解析]：由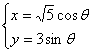

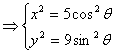
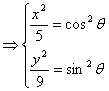
又因为，得+=1，

由此可得a=3，b=，c=2

所以准线方程．

16．（12分）

[解析]：因为椭圆经过点P（1，1），又以y轴为准线，所以椭圆在y轴的右边．

设椭圆中心Q．

而中心Q到准线的距离为．　

　　　　　 由椭圆的第二定义得

即椭圆的中心的轨迹方程是：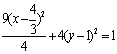

17．（12分）

[解析]：以y= x +t代入，并整理得　　①

因为直线与椭圆相交，则△=，

所以，即，

设A（），B（），则A（），B（），

且是方程①的两根．

由韦达定理可得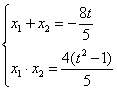：，　所以，弦长AB²=+

　　　　　　  =2　=2[]

　　　　　　  =2[]

得 AB=

所以当t=0时，AB取最大值为．

18．（12分）

[解析]：设所求椭圆的方程为，

依题意，点P（）、Q（）的坐标

满足方程组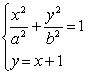

解之并整理得

或

所以，　　　　　 ①

　　　　　　　 ，　　　　　 ②

　　　 由OP⊥OQ　　　　　 ③

　　　 又由PQ==

　　　 =

　　　 =　　　　　　　④

　　　　由①②③④可得：

　　　　　　　　　　　 

　　　 故所求椭圆方程为，或

19．（14分）

[解析]：（1）由题设e=可得a²=4b²，

于是，设椭圆方程为

又设M（x，y）是椭圆上任意一点，且，

所以

　　　　 

因为，所以

①若b<，当y=-b时，有最大值为=

解得与b<相矛盾（即不合题意）．

②若b，当y=-时，有最大值为=

解得 b=1，a=2．

　　　　　 故所求椭圆方程为．

　　　　  （2） 把y=-代入中，解得，因此椭圆上的点（，），（，）到点P的距离都是

20．（14分）

[解析]：（1）设经过原点且倾斜角为的直线方程为y= x tan，代入，求得．由对称性可知四边ABCD为矩形，又由于，所以四边形ABCD的面积S=4 x y．

　　　　 （2）当时， ，设t=tan，则S，

　　　　  设，因为在（0，1]上是减函数，所以．

所以，当=时，．