（8）直线和圆
一、选择题（本大题共10小题，每小题5分，共50分）
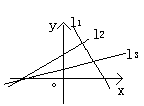1．如图所示，直线l1，l2，l3，的斜率分别为k1，k2，k3，则 （ ）
A． k1< k2< k3
B． k3< k1< k2
C． k3< kk2< k1
D． k1< k3< k2
2．点（0，5）到直线y=2x的距离是 （ ）
A． 
B． 
C． 
D．
3．经过点P（3，2），且倾斜角是直线x-4y+3=0的倾斜角的两倍的直线方程是
（ ）
A．8x-15y+6=0 B．x -8y+3=0
C．2x -4y+3=0 D．8x +15y+6=0
4．方程 x + y =1所表示的图形在直角坐标系中所围成的面积是 （ ）
A．2 B．
5．过点P（2，3），且在两坐标轴上的截距相等的直线方程是 （ ）
A．x +y-5=0或x -y+1=0 B．x -y+1=0
C．3x -2y=0或x +y-5=0 D．x -y+1=0或3x -2y=0
6．设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长，则直线sinA·x +ay+c=0与bx -sinB·y+sinC=0的位置关系是 （ ）
A．平行 B．重合 C．垂直 D．相交但不垂直
7．直线x -y+4=0被圆(x +2)2+(y-2)2=2截得的弦长为 （ ）
A． B． C．3 D．4
8．直角坐标系内到两坐标轴距离之差等于1的点的轨迹方程是 （ ）
A． x - y =1 B．x -y=1 C．( x - y )2=1 D． x -y =1
9．若集合
则a的取值范围是 （ ）
A．
B．
C．
D．
10．在约束条件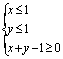
下，目标函数
的最小值和最大值分别是 （ ）
A．1，3 B．1，2 C．0，3 D．2，3
二、填空题（本大题共4小题，每小题6分，共24分）
11．如果直线l与直线x +y-1=0关于y轴对称，那么直线l的方程是 ．
12．直线
x +y-2=0截圆x2+y2=4，得劣弧所对的圆心角为
．
13．过原点的直线与圆x2+y2+4x +3=0相切，若切点在第三象限，则该直线的方程是 ．
14．如果直线l将圆：x2+y2-2x -4y=0平分，且不经过第四象限，则l的斜率的取值范围是
三、解答题（本大题共6小题，共76分）
15．求经过两点P1（2，1）和P2（m，2）（m∈R)的直线l的斜率，并且求出l的倾斜角α及其取值范围．（12分）
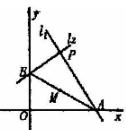
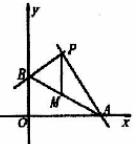
16．过点P(2,4)作两条互相垂直的直线l１，l２，若l１交x轴于A点，
l2 交y轴于B点，求线段AB的中点M的轨迹方程． （12分）
17．已知圆的半径为
，圆心在直线
上，圆被直线
截得的弦长为
，求圆的方程．（12分）
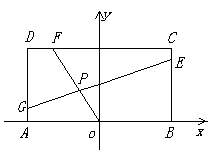18．已知常数
在矩形ABCD中，AB=4，BC=4
，O为AB的中点，点E、F、G分别在BC、CD、DA上移动，且
，P为GE与OF的交点（如图），求P点的轨迹方程.（12分）
19．要将甲、乙两种长短不同的钢管截成A、B、C三种规格，每根钢管可同时截得三种规格的短钢管的根数如下表所示：
| 规格类型
| A规格 | B规格 | C规格 | ||
| 甲种钢管 | 2 | 1 | 4 | ||
| 乙种钢管 | 2 | 3 | 1 |
今需A、B、C三种规格的钢管各13、16、18根，问各截这两种钢管多少根可得所需三种规格钢管，且使所用钢管根数最少． （14分）
20．已知圆的参数方程
（1）设
时对应的点这P，求直线OP的倾斜角；（2）若此圆经过点（m,1），求m的值，其中
；（3）求圆上点到直线
距离的最值．（14分）
参考答案
一．选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | A | A | C | C | B | C | D | A |
二．填空题（本大题共4小题，每小题6分，共24分）
11．x - y +1=0 12．
13．y=
x 14． [0，2]
三、解答题（本大题共6题，共76分）
15．（12分）
[解析]：(1)当m=2时，x 1＝x 2＝2，
∴直线l垂直于x轴，因此直线的斜率不存在，倾斜角α=
(2)当m≠2时，直线l的斜率k=
当m＞2时，k＞0．
∴α=arctan,α∈（0，），
当m＜2时，k＜0 ∴α＝π＋arctan，α∈(,π)．
16．（12分）
[解法1]：设点M的坐标为(x,y),
∵M为线段AB的中点，∴A的坐标为(2x,0)，B的坐标为(0，2y)，
∵l１⊥l２，且l１、l２过点P(2，4)，
∴PA⊥PB,kPA·ｋＰＢ＝－１．
而
整理，得x+2y-5=0(x≠1)
∵当x=1时，A、B的坐标分别为(2，0)、(0，4)．
∴线段AB的中点坐标是(1，2)，它满足方程x+2y-5=0，
综上所述，点M的轨迹方程是x+2y-5=0．
[解法2]：设M的坐标为(x,y)，则A、B两点的坐标分别
是(2x,0)、(0,2y)，连接PM，
∵l１⊥l２，∴2｜ＰＭ｜＝｜ＡＢ｜，
而｜ＰＭ｜＝
化简，得x+2y-5=0,为所求轨迹方程．
17．（12分）
[解析]：设圆心坐标为（m，2m）,圆的半径为
，所以圆心到直线x -y=0的距离为
由半径、弦心距、半径的关系得
所求圆的方程为
18．（12分）
[解析]：根据题设条件可知，点P(x，y)的轨迹即直线GE与直线OF的交点.
据题意有A（－2，0），B（2，0），C（2，4a），D（－2，4a）
设
，由此有E（2，4ak），F（2－4k，4a），G（－2，4a－4ak）.
直线OF的方程为：
，
①
直线GE的方程为：
. ②
从①，②消去参数k，得点P（x，y）的轨迹方程是：
，
19．（14分）
[解析]：设需截甲种钢管x根，乙种钢管y根，则
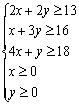作出可行域(如图)：
目标函数为z=x+y,
作直线l0：x+y=0，再作一组平行直线l：x+y=t，此直线经过直线4x+y=18和直线x+3y=16的交点A(
)，此时，直线方程为x+y=
．由于
和
都不是整数，所以可行域内的点()不是最优解．
经过可行域内的整点且与原点距离最近的直线是x+y=8,经过的整点是B(4，4)，它是最优解．
答：要截得所需三种规格的钢管，且使所截两种钢管的根数最少方法是，截甲种钢管、乙种钢管各4根．
20．（14分）
[解析]：（1）因为圆上任一点的坐标为（
，
），
所以当时，对应的点P的坐标为（
，
），即（-1，-）．所以直线OP的斜率为
，
所以直线OP的倾斜角为60°
（2）因为圆经过点（m,1），
所以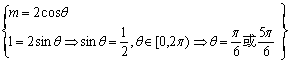
（3）设圆上的点P的坐标为（，），点P到直线的距离为
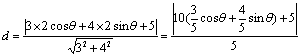
，其中
，
故最大值为3，最小值为0