（5）直线
一、选择题（本大题共10小题，每小题5分，共50分）
1．和直线3x-4y+5=0关于x轴对称的直线方程是 （ ）
A．3x+4y-5=0 B．3x+4y+5=
2．若直线的斜率k= -5，则倾斜角α= （ ）
A．arctan(-5) B． π-arctan(-5)
C．arctan5 D． π-arctan5
3．若直线ax+by+c=0过第一、二、三象限，则 （ ）
A．ab>0, bc>0 B．ab>0, bc<0
C．ab<0, bc>0 D．ab<0, bc<0
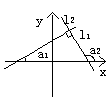
4．如图，直线l1的倾斜角a1=30°，直线l1⊥l2，则l2的斜率为 （ ）
A．-
B．
C．-
D．
5．若斜率为-2的直线l经过点（0，8），则l与两坐标轴围成的三角形面积为 （ ）
A．8 B．
6．若A（-2，3），B（3，-2），C（
，m）三点在同一直线上，则m的值为 （ ）
A．-2 B． D．
7．两条直线A1x+B1y+C1=0, A2x+B2y+C2=0垂直的充要条件是 （ ）
A． A
C． 
= -1 D． 
=1
8．已知两条直线l1：y= x, l2：ax -y=0，其中a为实数，当这两条直线的夹角在（0，
）内变动时，a的取值范围是 （ ）
A．（0，1） B．( , )
C．( 
, 1) ∪(1, ) D．(1, )
9．已知直线l1：y=-2x+3，l2：y==x-
，则l1、l2的夹角是
A．arctan3 B．arctan(-3) C．π-arctan3 D． π-arctan(-3)
10．已知直线l1：sinθ·x+cosθ·y+m=0， l2：x+cotθ·y+n=0 (θ为锐角，m，n∈R且m≠n)则l1与l2的位置关系是 （ ）
A．平行 B．垂直 C．重合 D．相交但不垂直
二、填空题（本题共4小题，每小题6分，共24分）
11．已知直线l的方程是kx-y+2+3k=0(k∈R)，则直线l必经过点 ．
12．若直线的倾斜角为π-arctan，且过点（1，0），则直线l的方程为
．
13．直线 2x-y-4=0绕它与x轴的交点逆时针旋转45°所得的直线方程是 ．
14．两条平行线3x+4y-12=0和6x +8y+6=0间的距离是 ．
三、解答题（本大题共6题，共76分）
15．求经过原点且经过以下两条直线的交点的直线的方程:
．(12分)
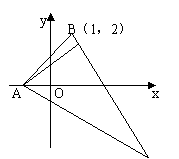
16．△ABC中，BC边上的高所在直线的方程为x-2y+1=0，∠A的平分线所在直线的方程为y=0，若点B的坐标为（1，2），求点A和点C的坐标．(12分)
17．已知两点A(－1,－5)，B(3,－2)，直线l的倾斜角是直线AB倾斜角的一半，求直线l的斜率． (12分)
18．在△ABC中，已知顶点A(1，1)，B(3，6)且△ABC的面积等于3，求顶点C的轨迹方程．
(12分)
19．光线从点A（2，3）射出，若镜面的位置在直线
上，反射线经过
B（1，1），求入射光线和反射光线所在直线的方程，并求光线从A到B所走过
的路线长．（14分）
20．如图，根据指令（γ，θ）（γ≥0，-180°<θ≤180°），机器人在平面上能完成下列动作：先原地旋转角度θ（θ为正时，按逆时针方向旋转θ，θ为负时，按顺时针方向旋转θ），再朝其面对的方向沿直线行走距离γ．
（1）现机器人在平面直角坐标系的坐标原点，且面对x轴正方向．试给机器人下一个指令，使其移动到点（4，4）．
（2）机器人在完成该指令后，发现在点（17，0）处有一小球 正向坐标原点作匀速直线滚动．已知小球滚动的速度为机器人直线行走速度的2倍，若忽略机器人原地旋转所需的时间，问机器人最快可在何处截住小球？并给出机器人截住小球所需的指令（结果用反三角函数表示）．（14分）
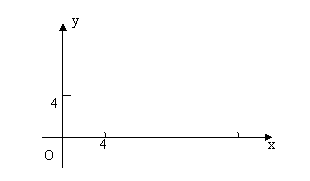
参考答案
一．选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | D | C | B | D | A | C | A | A |
二．填空题（本大题共4小题，每小题6分，共24分）
11．（-3，2） 12．x +2 y -1=0 13．3 x + y -6=0 14． 3
三、解答题（本大题共6题，共76分）
15．(12分)
[解析]:解方程组
所以, l1与l2的交点是(2,2)．
设经过原点的直线方程为
,把点(2,2)的坐标代入以上方程,得
,
所以所求直线方程为
（另：求直线交点与求直线方程的综合,求解直线方程也可应用两点式:
,即）
16．(12分)
[解析]：由 
得顶点A（-1，0）
又，AB的斜率
因为x轴是∠A的平分线，故AC的斜率为-1，
AC所在直线的方程为y =-( x +1) ①
已知BC上的高所在直线方程为x -2 y +1=0，故BC的斜率为-2，BC所在的直线方程为y -2=-2(x –1)②
联立①②解得顶点C的坐标为（5，-6）．
17．(12分)
[解析]：设直线l的倾斜角α，则由题得直线AB的倾斜角为2α．
∵tan2α=ｋAB=
即3tan2α+8tanα－3=0， 解得tanα＝
或tanα＝－3．
∵tan2α＝
＞0,∴0°＜2α＜90°, 0°＜α＜45°，
∴tanα＝．
因此，直线l的斜率是
18．(12分)
[解析]：设顶点C的坐标为(x,y),作CH⊥AB于H，则动点C属于集合
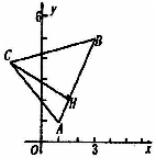P=｛Ｃ｜
｝，
∵ｋＡＢ＝
．
∴直线AB的方程是y-1=
(x-1),即5x-2y-3=0．
∴｜ＣＨ｜＝
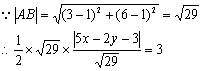
化简，得｜5x-2y-3｜=6,即5x-2y-9=0或5x-2y+3=0,这就是所求顶点C的轨迹方程．
19．（14分）
[解析]：设点A关于直线l的对称点为
垂直平分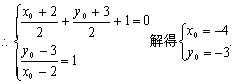 
在反射光线所在直线上．
反射光线的方程为
解方程组
得入射点的坐标为
．
由入射点及点A的坐标得入射光线方程为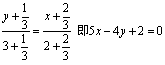
光线从A到B所走过的路线长为
20．(14分)
[解析]：（1）如图γ=
，θ=
，所下指令为（，）
（2）设机器最快在点P（x，0）处截住小球，则因为小球速度是机器人速度的2倍，所以在相同时间内有
即
因为要求机器人最快地去截住小球，即小球滚动距离最短，所以x =7,
故机器人最快可在点P（7，0）处截住小球，
又设Q（4，4），机器人在Q点旋转的角度为
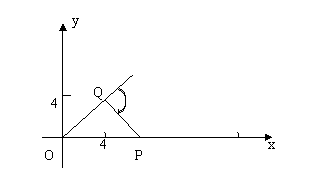则PQ
,
（法一）：由
∠QOP=45°，
∠QPx=
， -
（法二）： 
，
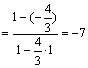
故，所给的指令为（5，
）或（5，
）