高二数学第二学期期中考试检测卷
———高二数学(文科) 选修1-2、4-4 (2007、4、28)
班级 姓名 座号 分数
一. 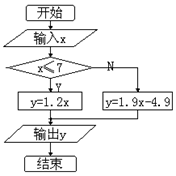 选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1、根据右边程序框图,当输入10时,输出的是( )
A.14.1 B.
2.已知集合M={1,![]() },
},
N={1,3},M∩N={1,3},则实数m的值为( )
A. 4 B. -
3、(1-![]() )
)![]()
![]() 等于 ( )
等于 ( )
A.2-2![]() B.2+
B.2+![]() C.-2 D.2
C.-2 D.2
4、若![]() 则复数
则复数![]() 表示的点在第( )象限.
表示的点在第( )象限.
A.一; B.二 C.三 D.四
5、右图是《集合》的知识结构图,如果要加入“子集”,则应该放在( )
 A.“集合的概念”的下位
A.“集合的概念”的下位
B.“集合的表示”的下位
C.“基本关系”的下位
D.“基本运算”的下位
6、由数列1,10,100,1000,……猜 测该数列的第n项可能是( )。
A.10n; B.10n-1; C.10n+1; D.11n.
7、直线:3x-4y-9=0与圆:![]() ,(θ为参数)的位置关系是( )
,(θ为参数)的位置关系是( )
A.相切 B.相离 C.相交但直线不过圆心 D. 直线过圆心
8、类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列
哪些性质,你认为比较恰当的是( )。
①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,
相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两
条棱的夹角都相等。
A.①; B.①②; C.①②③; D.③。
9、设![]() 大于0,则3个数:
大于0,则3个数:![]() ,
,![]() ,
,![]() 的值( )
的值( )
A.都大于2 B.至多有一个不大于2 C.都小于2 D.至少有一个不小于2
10、对于任意的两个实数对(a,b)和(c,d),规定(a,b)=(c,d)当且仅当a=c,b=d;运算
“![]() ”为:
”为:![]() ,运算“
,运算“![]() ”
”
为:![]() ,设
,设![]() ,若
,若![]()
则![]() (
)
(
)
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
二. 填空题(本大题共4小题,每小题5分,共20分.)
11、在复平面内,O是原点,向量![]() 对应的复数3+
对应的复数3+![]() ,如果A关于实轴的对称点B,
,如果A关于实轴的对称点B,
则向量![]() 对应的复数为
.
对应的复数为
.
12、把演绎推理:“所有9的倍数都是3的倍数,某个奇数是9的倍数,故这个奇数是3
的倍数”,改写成三段论的形式其中大前提: ,小前提:
,结论:
13、在研究身高和体重的关系时,求得相关指数![]() ______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
14、在极坐标系中,若过点(3,0)且与极轴垂直的直线交曲线![]() 于A、B两点,则AB=
。
于A、B两点,则AB=
。
三、 解答题(本大题共6小题,共80分.)
15、(本小题12分)实数m取什么值时,复数z=(m2-5m+6)+(m2-3m)![]() 是
是
(1)实数?(2)虚数?(3)纯虚数?
16、(12分)已知数列{an}的前n项和为Sn,![]() ,满足
,满足![]() ,
,
(1)求![]() 的值;(2)猜想
的值;(2)猜想![]() 的表达式。
的表达式。
17、(12分)已知![]() ,求证
,求证![]()
18、(14分)求以椭圆![]() 内一点A(1,-1)为中点的弦所在直线的方程。
内一点A(1,-1)为中点的弦所在直线的方程。
19、(16分)画出用二分法求方程![]() 的程序框图
的程序框图
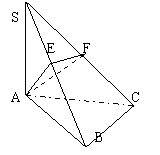
20、(14分)如图所示,![]() 面ABC,
面ABC,![]() ,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证:
,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证:![]()
 |
试卷答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | . B | D. | B | C | B | C | C | D | A |
二、填空题
11、![]() 12、所有9的倍数都是3的倍数,某个奇数是9的倍数,这个奇数是3
12、所有9的倍数都是3的倍数,某个奇数是9的倍数,这个奇数是3
的倍数 ;
13、![]() 14、
14、![]()
三、解答题
15、解:(1)当m2-3m=0, (1分)即m1=0或m2=3时,(3分)z是实数;(4分)
(2)当m2-3m≠0,(5分)即m1≠0或m2≠3时,(7分)z是虚数;(8分)
(3)当 (11分)即m=2时z是纯数;(12分)
(11分)即m=2时z是纯数;(12分)
16、解:(1)因为![]() ,且
,且![]() ,所以
,所以![]() (1分)
(1分)
解得![]() ,(2分)又
,(2分)又![]() (3分),解得
(3分),解得![]() ,(4分)又
,(4分)又![]() ,(5分)所以有
,(5分)所以有![]() (6分)
(6分)
(2)由(1)知![]() =
=![]() ,
,![]() ,
,![]() ,
,![]() (10分)
(10分)
猜想![]() (
(![]() )(12分)
)(12分)
17、证明:由![]() 得
得![]() (1分),即
(1分),即![]() (3分),即
(3分),即
![]() (4分),所以要证
(4分),所以要证![]() ,只要证
,只要证
![]() (6分),即证
(6分),即证![]()
(8分),即证![]() ①(10分),由
①(10分),由![]() 成立,所以①式成立,(11分)所以原等式得证(12分)
成立,所以①式成立,(11分)所以原等式得证(12分)
18、解:由已知条件可知所求直线的斜率![]() 存在且不为0(1分),故可设所求直线方程为:
存在且不为0(1分),故可设所求直线方程为:
![]() (3分),即
(3分),即![]() 代入椭圆方程
代入椭圆方程![]() 得:
得:
![]() ①(6分),设所求直线与已知椭圆的交点P、Q的坐标分别为
①(6分),设所求直线与已知椭圆的交点P、Q的坐标分别为![]() ,所以
,所以![]() 是方程①的两个根(7分),
是方程①的两个根(7分),
又因为点A(1,-1)是线段PQ的中点,所以有![]() (10分),
(10分),
即![]() (11分),解得
(11分),解得![]() (12分),所以所求直线的方程为
(12分),所以所求直线的方程为
![]() (14分)
(14分)
![]() 19、解: (1分)
19、解: (1分)
|
(2分)
![]()
(4分)
![]()
![]()
![]()
|
(6分)
![]()
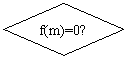 |
是
![]() (8分)
(8分)
![]()
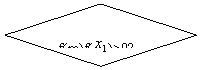 否
否
![]()
![]() 否 (10分)
否 (10分)
![]()
|
|
![]() (11分)
(11分)
![]()
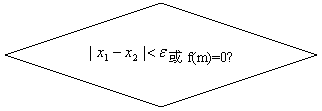 |
![]() 否
否
(14分)
![]()
![]() 是
是
![]() (15分)
(15分)
(16分)
![]()
20、证明:因为![]() 面ABC,所以
面ABC,所以![]() ,(3分) 又
,(3分) 又![]() 且
且![]() ,
,
所以![]() 面SAB,(6分) 所以
面SAB,(6分) 所以![]() AE,(8分) 因为
AE,(8分) 因为![]() 且
且![]() ,
,
所以![]() 面ABC,(11分)又因为
面ABC,(11分)又因为![]() ,所以根据三垂线定理可得
,所以根据三垂线定理可得![]() (14分)
(14分)
———高二数学(文科) 选修1-2、4-4 (2007、4、28)
班级 姓名 座号 分数
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二、 填空题(本大题共4小题,每小题5分,共20分.)
11、 ; 12、 , ,
;13、 ;14、
三、解答题(本大题共6小题,共80分.)