高二数学第二学期期中考试试卷

高二数学第二学期期中考试试卷

年级：高二　学科：数 学 　

一、选择题（本大题共12小题，每题5分，共60分，请将正确答案填入答题卷）

1．已知球的两个平行截面面积分别为和，它们位于球心的同一侧，且相距为1，则球半径为

A. 4　　　　　 　B．3　　　　　 C. 2　　　　　  D. 5

2. 、为异面直线，二面角——，，，如果二面角——的平面角为，则，所成的角为　　　　　

　A．　　　　　 　B．　　  C．或　　 D．

3. 下面有四个命题：①各个侧面都是等腰三角形的棱锥是正棱锥；②三条侧棱都相等的棱锥是正棱锥；③底面是正三角形的棱锥是正三棱锥；④顶点在底面上的正射影是底面多边形的内心，又是外心的棱锥必是正棱锥.其中正确命题的个数是.

A. 1　　　　　 　B．2　　　　　 C. 3　　　　　  D.4

4．已知平面∥平面，直线平面,点P直线,平面、间的距离为8，则在内到点P的距离为10，且到的距离为9的点的轨迹是

A.一个圆　　 　 B.四个点　　　 C.两条直线　　　D. 两个点

5． 和是两个不重合的平面，在下列条件中可判定平面和平行的是

A. 内不共线的三点到的距离相等　　B.是平面内的直线且

C. 和都垂直于平面γ　　　 D.是两条异面直线且

6．一个四面体的所有棱长都为，四个顶点在同一球面上，则此球的表面积为　　　

　　　A．3π　　　　　　　　　　B．4π　　　　　　　　 C．　　　　　　　　 D．6π　　　　 　　　　　　　　　 

7．考察下列命题：

　　　（1）掷两枚硬币，可能出现“两个正面”、“两个反面”、“一正一反”3种结果；

　　　（2）某袋中装有大小均匀的三个红球、二个黑球、一个白球，那么每种颜色的球被摸到的可能性相同；

　　　（3）从中任取一数，取到的数小于0与不小于0的可能性相同；

　 （4）分别从3个男同学、4个女同学中各选一个作代表，那么每个同学当选的可能性相同；

　其中正确的命题有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　A．0个　　　　　　　　 B．1个　　　　　　C．2个　　 　　　D．3个

8．△ABC的BC边上的高线为AD，BD=a，CD=b，将△ABC沿AD折成大小为θ的二面角B-AD-C，若，则三棱锥A-BCD的侧面三角形ABC是

A．锐角三角形　　　　　　  　 B．钝角三角形

C．直角三角形　　　　　　  　 D、形状与a、b的值有关的三角形

9．设 求的值是（　 ）

A．2或3或4　　　 B．4或7或11　　 C．只有3　　　 D．只有7

10．…除以88的余数是　　　　　

A． －1　　 　　　 B．－87　　 　　  C． 1　　　　　　D．87

11. 定义,其中i,n,且i≤n,　　　　　　　　　

若=的值为

　A．2　　　　　　 　 B．0　 　　　　 　C．－1　　　　   D．－2

12．四面体的顶点和各棱中点共有10个点，取其中4个不共面的点，则不同的取法共有

A．150种　　　　　　B．147种　　　　 C．144种　　　  D．141种

二、填空题（本大题共4小题，共16分，请将正确答案填入答题卷）

13．在的展开式中,二项式系数的和是 　　　　.　　

14．从装有两个白球、两个黑球的袋中任意取出两个球，取出一个白球一个黑球的概率为　　　　　　　　　．

15. 在北纬45°线上有A、B两点，点A在东经120°，点B在西经150°，设地球半径为R，则A、B两地的球面距离是 　　　　　　　　.

16. 有下列四个命题：①过平面α外两点有且只有一个平面与平面α垂直；②互相平行的两条直线在同一平面内的射影必是平行线；③直线l上两个不同点到平面α的距离相等是∥α的必要非充分条件；④平面α内存在无数条直线与已知直线l垂直是的充分非必要条件.其中正确命题的序号是　　　　　　　　　   

年级：高二  学科：数 学 　

题号	一	二	三						总分
			17	18	19	20	21	22
得分

一、选择题（本大题共12小题，每题5分，共60分

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题（本大题共4小题，共16分）

13、___________ __　 ___.　　　　　　　　  14. _______________　  __.

15、_______________　　_.　　　　　　　　  16、________________　　_.

三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.

17. （本题满分12分）

若平面α内的直角△ABC的斜边AB=20,平面α外一点O到A、B、C三点距离都是25,求：点O到平面α的距离．

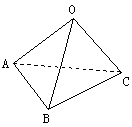
座位号

18．（本题满分12分）

甲、乙、丙三人值周，从周一至周六，每人值两天，但甲不值周一，乙不值周六，问可以排出多少种不同的值周表 ？

19．（本题满分12分）

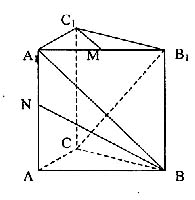如图所示在直三棱柱ABC—A₁B₁C₁中，CA=CB=l，∠BCA=90°，侧棱AA₁=2，M、N分别为A₁B₁，A₁A的中点

(1) 求的长；

(2) 求的值；

(3)求证：A₁B⊥C₁ M

20．（本题满分12分）

已知()ⁿ的展开式中前三项的二项式系数的和等于37，求展式中二项式系数最大的项的系数.

21．（本题满分12分）

由－1，0，1，2，3这5个数中选3个不同的数作为二次函数y=ax2+bx+c的系数.

（1）开口向上且不过原点的抛物线有几条？

（2）与x轴的负半轴至少有一个交点的抛物线有多少条？

22．（本题满分14分）

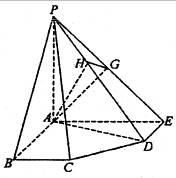
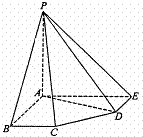在五棱锥P-ABCDE中，PA=AB=AE=2a，PB=PE=a，BC=DE=a，∠EAB=∠ABC=∠DEA=90°．

（1）求证：PA⊥平面ABCDE；

（2）求二面角A-PD-E的大小；

（3）求点C到平面PDE的距离．

高 二 数 学 答 案

一.BCABD　AACBC DD

二.13.  14．　15. 　16. ③

17. 解：由斜线相等，射影相等知，O在底面的射影为△ABC的外心Q，

又△ABC为Rt△外心在斜边中点，故OQ===

18. 解法一：（排除法）．

解法二：分为两类：一类为甲不值周一，也不值周六，有；

另一类为甲不值周一，但值周六，有，

∴一共有+＝42种方法．

19．解：建立空间直角坐标系如图，

（1）依题意得B（0，1，0）、N（1，0，1），则

；

（2）A₁（1，0，2），B（0，1，0），C（0，0，0），B₁（0，1，2），

则

 

所以；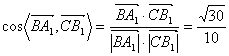

（3）证明：依题意，得C₁（0，0，2）、M（，，2）、

=（，，0），则，

∴，即A₁B⊥C₁M

20．解：由　得　 得．

　 ，该项的系数最大，为

21.解析：（1）抛物线开口向上且不过原点，记，

∴ 选a的时候有3种选法，再选c的时候也只有3种，最后选b也有3种，

　　　由分步计数原理有抛物线3×3×3=27条。　　　

（2）与x轴的负半轴至少有一个交点的抛物线对应的根的情况是：

（i）两个负根：，又a，b，c不相同，

　　　故（a，b，c）满足条件的有：（2，3，1），（1，3，2）两个；　

（ii）一负根一正根：，∴ ac＜0即可，共有3×1×3×2＝18条抛物线；

（iii）一负根一零根：，此时共有＝6种情况.

22.（1）证明∵PA=AB=2a，PB=2a,　 ∴PA²+AB²=PB²，∴∠PAB=90°，即PA⊥AB．

同理PA⊥AE．　　　　　　　∵AB∩AE=A，∴PA⊥平面ABCDE．

　 （2）∵∠AED＝90°，∴AE⊥ED．∵PA⊥平面ABCDE，

∴PA⊥ED．∴ED⊥平面PAE．过A作AG⊥PE于G，

过DE⊥AG，∴AG⊥平面PDE．过G作GH⊥PD于H，连AH，

由三垂线定理得AH⊥PD．∴∠AHG为二面角A-PD-E的平面角．　　　　　　

 在直角△PAE中，AG＝a．在直角△PAD中，AH＝a，

∴在直角△AHG中，sin∠AHG＝＝．∴∠AHG＝arcsin．

（3）∵∠EAB=∠ABC=∠DEA=90°,　 BC=DE=a,AB=AE=2a,

　 取AE中点F，连CF，　 ∵AF∥=BC,

　 ∴四边形ABCF为平行四边形．　 ∴CF∥AB，而AB∥DE，

　 ∴CF∥DE，而DE平面PDE，CF平面PDE，

　 ∴CF∥平面PDE．

　 ∴点C到平面PDE的距离等于F到平面PDE的距离．

　 ∵PA⊥平面ABCDE，　 ∴PA⊥DE．

　 又∵DE⊥AE，∴DE⊥平面PAE．

　 ∴平面PAE⊥平面PDE．∴过F作FG⊥PE于G，则FG⊥平面PDE．

　 ∴FG的长即F点到平面PDE的距离．　　　　　　　　　　　　　　　　　　　　　　　

　　 在△PAE中，PA=AE=2a，F为AE中点，FG⊥PE，

　 ∴FG=a． ∴点C到平面PDE的距离为a．　　 (或用向量法)