圆锥曲线-----抛物线
一 基础热身
1.点M与点F
的距离比它到直线:
的距离小1,则点
的轨迹方程是
___________.
2.抛物线
的焦点的坐标是
, 准线方程是
.
3.设直线
经过抛物线
的焦点,与抛物线相交于A
,B
两点,(1)
= ;(2)
= ;
(3)若直线的斜率为1,则
=
;(4) 
= .(5)通径是________.
4.过A（－1，1），且与抛物线
有一个公共点的直线方程为
。
二 典例回放
1.求顶点在原点，以坐标轴为对称轴，且焦点在直线3x-4y=12上的抛物线方程.
2.已知圆
与顶点原点O，焦点在x轴上的抛物线交于A、B两点，△AOB的垂心恰为抛物线的焦点，求抛物线C的方程。
3.过抛物线
的顶点作互相垂直的二弦OA、OB。求(1)AB中点的轨迹方程。(2)证明：AB与x轴的交点为定点。
三 水平测试
1.抛物线的顶点在原点,对称轴是x轴,点(－5,2
)到焦点距离是6,则抛物线的方程为（ ）
（A）
（B）
（C） （D）
2.一个正三角形的顶点都在抛物线上，其中一个顶点在原点，则这个三角形的面积是（ ）
（A）
（B）
（C）
（D）
3.抛物线
截直线
所得弦长等于
（ ）
A.
（B）
（C）
（D）15
4.抛物线
上有
三点,
是它的焦点,若
成等差数列,则
（A）
成等差数列 （B）
成等差数列 （C）
成等差数列 （D）
成等差数列
5.若双曲线
的一条准线与抛物线
的准线重合，则双曲线的离心率e为（ ）
（A）
（B）2
（C）4
（D）4
6.已知圆
，与抛物线的准线相切，则
___________．
7.若点A的坐标是（3，2），F为抛物线y2=2x的焦点，点M在抛物线上移动时，使MA+MF取最小值的M的坐标为______.
8.已知抛物线的顶点在坐标原点，对称轴为x轴，且与圆x2+y2=4相交的公共弦长等于2
，求这抛物线的方程。
9.给定直线：
，抛物线C：
。
(1)当抛物线C的焦点在直线上时，确定抛物线C的方程。
(2)若△ABC的三个顶点都在（1）所确定的抛物线C上，且点A的纵坐标
，△ABC的重心恰在抛物线C的焦点上，求直线BC的方程。
答案：一 基础热身：1。
2。
3。1 -4 8 -3 4
4．
及X=-1
二． 典例回放：
1.
解:直线L与X轴交点(4,0),与Y轴交点(0,-3)所以抛物线方程为
2. 解：设所求抛物线
，因为△AOB的垂心恰为抛物线的焦点,所以AB⊥X轴,则可设A
,
,
.而
,
,由题意
,可得
,即
.又A点既在圆上又在抛物线上所以
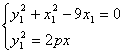得
所以
,
3. 解(1)设
,
,则
,代入抛物线方程得:
,及
.又OA⊥OB,
.得
(舍),而
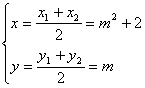消去M:
(2)在直线方程中,令
得
所以交点为(2,0)
三 水平测试:1.D 2.A 3.A 4.A 5.A 6.2 7.(2,2)
8.解:设抛物线方程为
.当
时,根据对称性设
,
,代入圆方程得
,
,求得抛物线方程为
.同理可得
9.(1) 
(2)
代入得
则A(8,2),设
.
直线方程代入,由韦达定理及重心坐标公式
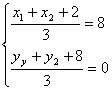求得
.