高二数学圆锥曲线-椭圆练习

圆锥曲线------椭圆

一 基础热身

1.已知两个定点,,(1)若=10,则点的轨迹方程是　　　　 .(2)若=8, 则点的轨迹方程是　　　　 .(3)若=6, 则点的轨迹方程是　　　　 .

2.椭圆的长轴与半短轴的和等于　　　 , 离心率等于　　　 , 焦点的坐标是　　　　　　　　　 ,顶点的坐标是　　　　　　　　　　　　　  ,准线方程是　　　　　　  ,左焦点到右准线的距离等于　　　　　  .通径是__________.

3.点P与定点F（4，0）的距离和它到定直线的距离之比是4：5，则点P的轨迹方程是_____________.

4.已知方程表示焦点在轴上的椭圆，则的取值范围是_______________.

5.直线与椭圆相交于A,B两点,则=　　　　  .

二 典例回放

1.中心在原点，一焦点为的椭圆被直线截得的弦的中点的横坐标为，求此椭圆的方程。

2.已知抛物线y²＝4x，椭圆，它们有共同的焦点F₂，若P是两曲线的一个公共点，且F₁是椭圆的另一个焦点，求△PF₁F₂的面积．

3.是椭圆中不平行于对称轴的一条弦，是的中点，是椭圆的中心，求证：为定值．

三 水平测试

1.如果椭圆4x²＋y²=k上两点间的最大距离是8，那么k等于（　）。

（A）32　　（B）16　　（C）8　　（D）4

2若过椭圆左焦点的弦PQ垂直于长轴，且⊥，则椭圆的离心率为（　）。

（A）＋1　（B）－1　（C）(2－)　（D）(－1)

3.已知椭圆内有一点P(1, －1), F₁为椭圆的右焦点，M为椭圆上的点，且使MP＋2MF₁之值最小，则M点的坐标是（　）。

（A）(, －1)　（B）(1, ±)　（C）(1, －) （D）(±, －1)

4.曲线与曲线之间具有的等量关系　（　　　）

　 有相等的长、短轴 　有相等的焦距　 有相等的离心率　　　有相同的准线

5.椭圆的两个焦点为F₁、F₂，过F₁作垂直于x轴的直线与椭圆相交，一个交点为P，则=（　 ）.

(A)　　　　　　　  (B)　　　　　　　  (C)　　　　　　　　(D)4

6.若分别表示椭圆的长半轴、短半轴，半焦距及焦点到对应准线的距离，则(　　)

(A)　　　　　 (B)　　　　  (C)　　　　　　 (D)

7.已知椭圆的长轴长是短轴长的倍，长、短轴都在坐标轴上，且过点，则椭圆的方程是　　　 ．

8.底面直径为的圆柱被与底面成的平面所截，截口是一个椭圆，这个椭圆的长轴长　　　　　  ，短轴长　　 ，离心率　　　　  ．

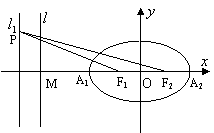
9. (05浙江)　17．如图，已知椭圆的中心在坐标原点，焦点F₁，F₂在x轴上，长轴A₁A₂的长为4，左准线l与x轴的交点为M，MA₁∶A₁F₁＝2∶1．

　 (Ⅰ)求椭圆的方程；

　 (Ⅱ)若直线l₁：x＝m(m＞1)，P为l₁上的动点，使∠F₁PF₂最大的点P记为Q，求点Q的坐标(用m表示)．

　　　　　　　　　　  　　　　　　　　　　　

答案：一 基础热身：

1．　　　　　　　　 无

2．14，　 （-3，0）（3，0）　　　（5，0）（-5，0）（0，4）（0，-4）　　

3．　　　　4.　　 5.

二 典例回放

　 1.　　  2.　　 

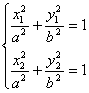　 3.设：　则：　而 两式相减得

三 水平测试：

　 1.B　　 2.B　　 3.A　　 4.B　　 5.C　　 6.D　　 7.或　　

　 8.　 12　

9.