高二数学圆锥曲线-轨迹练习

圆锥曲线-----轨迹

一 基础热身

1.点与点的距离比它到直线的距离小，则点的轨迹方程是______________.

2.一动圆与圆外切，而与圆内切，则动圆圆心的轨迹方程是　　　　　  _______

3.已知椭圆的两个焦点分别是F₁，F₂，P是这个椭圆上的一个动点，延长F₁P到Q，使得｜PQ｜＝｜F₂P｜，求Q的轨迹方程是　　　　　　　　 ．

4.倾斜角为的直线交椭圆于两点，则线段中点的轨迹方程是　　　 _______.

5.平面直角坐标系中，O为坐标原点，已知两点A（3，1），B（-1，3），若点C满足，其中，且，则点C的轨迹方程为____________________.

二 典例回放

1.⊙C：内部一点A（，0）与圆周上动点Q连线AQ的中垂线交CQ于P，求点P的轨迹方程.

2.一条曲线在x轴上方，它上面的每一个点到点的距离减去它到x轴的距离的差都是2，求这条曲线的方程。

3.△ABC中，B（－3，8）、C（－1，－6），另一个顶点A在抛物线y²=4x上移动，求此三角形重心G的轨迹方程.

4.抛物线 y²=2px(p>0)，O为坐标原点，A、B在抛物线上，且OA⊥OB，求弦AB中点Ｍ的轨迹方程．

三 水平测试

1.与两点距离的平方和等于38的点的轨迹方程是（　　 ）

　　　　 　　 

2.过椭圆4x²+9y²=36内一点P(1,0)引动弦AB,则AB的中点M的轨迹方程是()

(A)4x²+9y²-4x=0　 (B)4x²+9y²+4x=0　　　(C)4x²+9y²-4y=0　　　(D)4x²+9y²+4y=0

3.若,则点的轨迹是(　　)

　（Ａ）圆　　　（Ｂ）椭圆　　　（Ｃ）双曲线　　　（Ｄ）抛物线

４.已知M（－2，0），N（2，0），PM－PN=4，则动点P的轨迹是：（）

双曲线　　 双曲线左支　　 一条射线　　 双曲线右支

５.已知三角形ABC中， 则点A的轨迹是________________.

６.抛物线ｙ＝x²＋2mx+m²+1-m的顶点的轨迹方程为_________________________.

７.线段AB的两端点分别在两互相垂直的直线上滑动，且，求AB的中点P的轨迹方程。

８.已知两点M（-1，0）、N（1，0），且点P使，，成公差小于零的等差数列。

（1）、点P的轨迹是什么曲线？

（2）、若点P坐标为，记为与的夹角，求。

答案：一 基础热身

1．　　2。　　 3。　　 4。（椭圆内部）　　 5.

二 典例回放:

1.　　　　　　  解:设,由题意,. P的轨迹为C,A为焦点的椭圆的一部分,即: （椭圆内部）

2.　　　　　　  　　3.由重心坐标公式及转移代入法得:

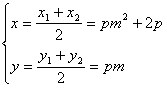3.　　　　　　  设:直线代入得:,由韦达定理及可求得.再由消去

(抛物线内部)

三 水平测试:

　 1.B　　　2.A　　3.C　　　４Ｃ　　　５．圆　　　６．　　　７．

　９．（１）　　　（２）设，

而
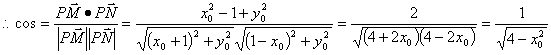