高二数学同步测试（12）—圆锥曲线综合
一、选择题（本大题共10小题，每小题5分，共50分）
1．椭圆
(a>b>0)离心率为
,则双曲线
的离心率为 （ ）
A．
B．
C．
D．
2．抛物线顶点在原点，焦点在y轴上，其上一点P(m，1)到焦点距离为5，则抛物线方程为
（ ）
A．
B．
C．
D．
3．圆的方程是(x－cosq)2+(y－sinq)2= ,当q从0变化到2p时，动圆所扫过的面积是 （ ）
A．
B．p C．
D．
4．若过原点的直线与圆
+
+
+3=0相切，若切点在第三象限，则该直线的方程是 （
）
A．
B．
C．
D．
5．椭圆
的焦点为F1和F2，点P在椭圆上，如果线段PF1中点在y轴上，那么PF1是PF2的
（ ）
A．7倍 B．5倍 C．4倍 D．3倍
6．以原点为圆心，且截直线
所得弦长为8的圆的方程是 （ ）
A．
B．
C．
D．
7．曲线
（
为参数）上的点到原点的最大距离为 （ ）
A．
1
B．
C．2
D．
8．如果实数x、y满足等式
，则
最大值
（ ）
A．
B．
C．
D．
9．过双曲线x2－
=1的右焦点F作直线l交双曲线于A, B两点，若AB=4，则这样的直线l有
（ ）
A．1条 B．2条 C．3条 D．4条
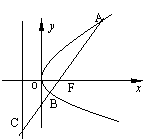10．如图，过抛物线
的焦点F的直线
交抛物线于点A．B，交其准线于点C，若
，且
，则此抛物线的方程为
（ ）
A．
B．
C．
D．
二、填空题（本大题共4小题，每小题6分，共24分）
11．椭圆的焦点是F1（－3，0）F2（3，0），P为椭圆上一点，且F1F2是PF1与PF2的等差中项，则椭圆的方程为_____________________________．
12．若直线
与圆
没有公共点，则
满足的关系式为 ．
以（
为点P的坐标，过点P的一条直线与椭圆
的公共点有
个.
13．设点P是双曲线
上一点，焦点F（2，0），点A（3，2），使PA+
PF有最小值时，则点P的坐标是________________________________．
14．AB是抛物线y=x2的一条弦，若AB的中点到x轴的距离为1，则弦AB的长度的最大值为 .
三、解答题（本大题共6小题，共76分）
15．P为椭圆
上一点，
、
为左右焦点，若
（1） 求△
的面积；
（2） 求P点的坐标．（12分）
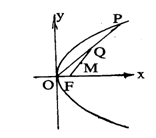16．已知抛物线
，焦点为F，顶点为O，点P在抛物线上移动，Q是OP的中点，M是FQ的中点，求点M的轨迹方程．（12分）
17．已知焦点在
轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点
为圆心，1为半径的圆相切，又知C的一个焦点与A关于直线
对称．
（1）求双曲线C的方程；
（2）设直线
与双曲线C的左支交于A，B两点，另一直线
经过M（－2，0）及AB的中点，求直线在
轴上的截距b的取值范围．（12分）
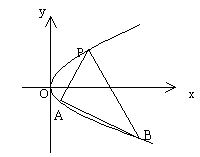
18．如图，过抛物线
上一定点P（
）（
），作两条直线分别交抛物线于A（
），B（
）．
（1）求该抛物线上纵坐标为
的点到其焦点F的距离；
（2）当PA与PB的斜率存在且倾斜角互补时，求
的值，并证明直线AB的斜率是非零常数.（12分）
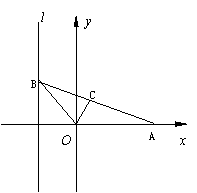
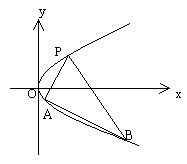
19．如图，给出定点A(
, 0) (>0)和直线: x = –1
. B是直线l上的动点，ÐBOA的角平分线交AB于点C.
求点C的轨迹方程，并讨论方程表示的曲线类型与值的关系.（14分）
 |
20．椭圆C1：
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2：
=1在第一象限内的图象上一点，直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等．
（1）求P点的坐标；
（2）能否使直线CD过椭圆C1的右焦点，若能，求出此时双曲线C2的离心率，若不能，请说明理由.（14分）
参考答案
一、选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | A | C | A | B | C | D | C | B |
二、填空题（本大题共4小题，每小题6分，共24分）
11．
12．
, 2 13．
14． 
三、解答题（本大题共6题，共76分）
15．（12分）
[解析]：∵a＝5，b＝3
c＝4
（1）设
，
，则
①
②，由①2－②得
（2）设P
，由
得
4
，将
代入椭圆方程解得
，
或
或
或
16．（12分）[解析]：设M（
），P（
），Q（），易求的焦点F的坐标为（1，0）
∵M是FQ的中点，∴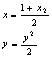 
，又Q是OP的中点∴ 
，
∵P在抛物线
上，∴
，所以M点的轨迹方程为
.
17．（12分）
[解析]：（1）当
表示焦点为
的抛物线；（2）当
时，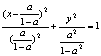
，表示焦点在x轴上的椭圆；（3）当a>1时，
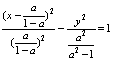，表示焦点在x轴上的双曲线. （1设双曲线C的渐近线方程为y=kx，则kx-y=0∵该直线与圆
相切，∴双曲线C的两条渐近线方程为y=±x．故设双曲线C的方程为
．
又双曲线C的一个焦点为
，∴
，
．∴双曲线C的方程为:
.
（2）由
得
．令
∵直线与双曲线左支交于两点，等价于方程f(x)=0在
上有两个不等实根．
因此
，解得
．又AB中点为
，
∴直线l的方程为：
． 令x=0，得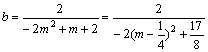
．
∵
，∴
，∴
．
18．（12分）[解析]：（I）当
时，
又抛物线
的准线方程为
由抛物线定义得，所求距离为
（2）设直线PA的斜率为
，直线PB的斜率为
由
，
相减得
,故
同理可得
,由PA，PB倾斜角互补知
即
,所以
, 故
设直线AB的斜率为
,由
，
,相减得
所以
, 将
代入得
，所以是非零常数.
19．（14分）[解析]：设B（－1，b），
：y=0, 
:y=－bx,设C（x,y），则有
<a，由OC平分ÐBOA，知点C到OA，OB距离相等，
①及C在直线AB: 
②上，由①②及
得，得
若y=0,则b=0 满足
.
20．（14分）[解析]：（1）设P(x0,y0)(x0>0,y0>0)，又有点A(－a,0),B(a,0).
，
又
，
，
.
（2）
代入
，
∴CD垂直于x轴.若CD过椭圆C1的右焦点，则
故可使CD过椭圆C1的右焦点，此时C2的离心率为
.