导数定义基础测试
一、选择题
1.设函数
，当自变量x由1变到1.1时，函数的平均变化率（ ）
A．2.1 B．
解析：
，故选A
2.函数
在x=0处的导数是 （ ）
A.0 B
解析：根据导数定义可得
,则当x=0时
，故选A
3.已知函数f(x)在x=1处的导数为1，则 
= ( )
A．2 B．
D．
解析：
，故选B.
4．若曲线y=f (x)在点(x0, f(x0))处的切线方程为2x－y+1=0，则（ ）
（A）f ’(x0)>0 （B）f ’(x0)<0 （C）f ’(x0)=0 （D）f ’(x0)不存在
解析：曲线在点(x0, f(x0))处的导数就是切线的斜率，因为直线2x－y+1=0的斜率为2，则
，故选A.
5．设曲线
在点P处的切线斜率为3，则点P的坐标为 （ ）
A．（3，9） B．（－3，9） C．（
） D．（
）
解析：曲线在点P处切线斜率即在该点的导数，故求导数为3的点既可.因为的导数为
，则x=
,故P点坐标为（，
），故选C.
6、给出下列命题：
（1）若函数y=x，则当x=0时
（2）若函数f(x)=2x2+1，图象上P(1,3)及邻近上点Q(1+Δx,3+Δy)，
则
=4+2Δx
（3）加速度是动点位移函数S(t)对时间t的导数；
其中正确的命题有（ ）
A. 0个 B.1个 C.2个 D。3个
解析：因为y=x的导数为y=1，故（1）错；（2）正确；（3）速度是动点位移函数S(t)对时间t的导数，加速度是速度函数关于时间t的导数.故选B.
7. 某物体的运动方程为
（位移单位：m，时间单位：s）它在t＝2s时的瞬时速度为（ ）
A. 5 B.
解析：物体的瞬时速度就是物体在该点函数的导数，根据导数的定义可以求得函数的导数为
，故当t=2时，
，则速度为20，故选D
8
．函数
A．4x+3
B．4x
解析： 
，则
，则函数的导数为
=4x-3，故选D.
二、填空题
9.若函数
，则
＝
.
解析：
，所以-8的导数，即常数的导数为0.故=0.
10
,
.
解析： 因为
的导数为
，则当x=1时，
=-2.
11..曲线
在（1，）处切线的方程是
.
解析：因为的导数为
，所以在点（1，）的切线斜率为1，故切线的方程为
.
三、解答题
12.求下列函数的导数
（1）
（2）
；
分析：按照函数求导的三个步骤
解：（1）
所以
.
（2）
所以
讲评：注意符号和步骤的规范.
13某物体的运动方程为（位移单位：m，时间单位：s）求它在t＝2s时的瞬时速度.
分析：求物体的瞬时实质就是求对应函数在该时刻的导数.
解：由导数的定义，在t=20的瞬时速度为
=
因为t=2，所以v=20(m/s)
答：物体在t＝2s时的瞬时速度为20m/s.
14.已知抛物线 
与直线y = x + 2.
求：（1）两曲线的交点； （2）抛物线在交点处的切线方程。
分析：两曲线的交点，即方程组的解；求出交点，根据交点导数即可求出切线方程.
解：（1） 
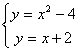
（2）
当交点为（3，5）时，=6，故切线方程为：
当交点为（-2，0）时，=-4，故切线方程为：
15在抛物线
上，哪一点的切线处于下述位置？
（1）与x轴平行
（2）平行于第一象限角的平分线.
（3）与x轴相交成45°角
分析：求抛物线的切线实质就是求函数的导数.
解：
（1）
当切线与x轴平行时，导数，即
，所以在点（0，2）的切线与x轴平行时.
（2）
当切线平行于第一象限角的平分线，导数
，即
，所以在点（
，
）的切线平行于第一象限角的平分线.
（3） 与x轴相交成45°角，导数为1或-1，
若导数，即，求得点为（，）.
若导数，即
，求得点为（，）
所以在点（，）、（，）与x轴相交成45°角.