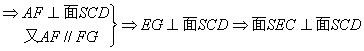高二数学直线平面几何体单元检测题
命题人:程浩 学号________. 姓名________.
一.选择题 (每小题5分,共50分)
1. 已知向量![]() ,且
,且![]() 与
与![]() 互相垂直,则
互相垂直,则![]() 的值是
的值是
A.1 B.![]() C.
C.![]() D.
D.![]()
2. 棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为
![]()
3. 设O、A、B、C是不共面的四点,对于空间一点P,使四点P、A、B、C共面的条件是
![]()
![]()
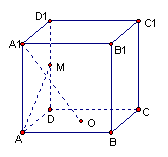 如图,正方体AC1中,M是棱D1D的中点,O是正方形ABCD的中心,则异面直线OA1与AM所成的角是
如图,正方体AC1中,M是棱D1D的中点,O是正方形ABCD的中心,则异面直线OA1与AM所成的角是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. ![]()
![]()
8. 正方体ABCD–A1B
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9. 设三点A(1,1,0),B(1,0,1),C(0,1,1),则△ABC的形状为
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
10. 在侧棱长为a的正四棱锥中,棱锥的体积最大时底面边长为
A.![]() a B.
a B.![]() a C.
a C.![]() a D.a
a D.a
第Ⅱ卷(非选择题 共5道填空题6道解答题)
请将你认为正确的答案代号填在下表中
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二.简答题 (每小题5分,共25分)
11. 把函数![]() 的图象沿向量
的图象沿向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是__________
可以是__________
12. 已知平面α⊥β, ![]() =
=![]() ,P是空间一点,且P到α、β的距离分别是1、2,则点P到
,P是空间一点,且P到α、β的距离分别是1、2,则点P到![]() 的距离为
。
的距离为
。
13. 与![]() 共线且满足方程
共线且满足方程![]() 的向量
的向量![]() __________
__________
14. 某地球仪上北纬![]() 纬线的长度为
纬线的长度为![]() ,该地球仪的半径是__________cm,表面积是______________cm2.
,该地球仪的半径是__________cm,表面积是______________cm2.
15. 设A(1,2,-1),B(0,3,1),C(-2,1,2)是平行四边形的三个顶点,则此平行四边形的面积为__________________.
三.解答题 (共75分)
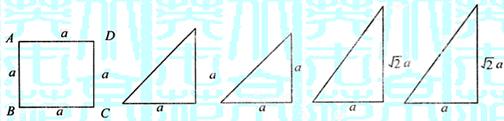
16. 下面的一组图形为某一四棱锥S—ABCD的侧面与底面;
|
(1)请画出四棱锥S—ABCD的示意图. 是否存在一条侧棱垂直于底面?如果存在,请给出证明;
(2)若SA⊥面ABCD,E为AB中点,求二面角E—SC—D的大小;
(3)求点D到面SEC的距离.
17. 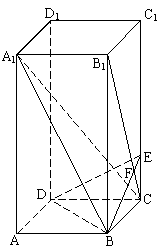 如图,已知正四棱柱ABCD—A1B
如图,已知正四棱柱ABCD—A1B
⑴求证:A
⑵求A1B与平面BDE所成的角的正弦值.
18. 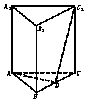 如图正三棱柱,棱都相等,D是BC上一点,AD⊥C1D.
如图正三棱柱,棱都相等,D是BC上一点,AD⊥C1D.
(1)求证:截面ADC1⊥侧面BCC1B1.
(2)求二面角CAC1D的大小.
(3)若AB=2,求A1B与截面ADC1的距离.
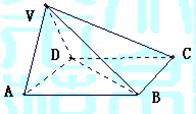
19. 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD;
|
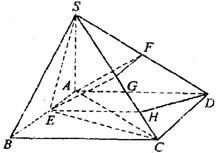
20. 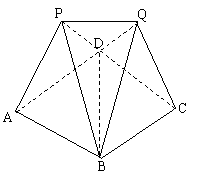 如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面![]() 内作菱形ABCD,其边长为1,∠BAD=60°,再在平面
内作菱形ABCD,其边长为1,∠BAD=60°,再在平面![]() 的上侧,分别以△ABD与△CBD为底面安装上相同的正三棱锥P-ABD与Q-CBD,∠APB=90°。
的上侧,分别以△ABD与△CBD为底面安装上相同的正三棱锥P-ABD与Q-CBD,∠APB=90°。
⑴求证:PQ⊥BD;
⑵求二面角P-BD-Q的大小;
⑶求点P到平面QBD的距离。
21. 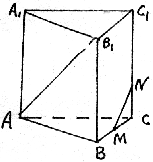 已知正三棱柱ABC-A1B
已知正三棱柱ABC-A1B
(直线平面几何体)单元检测题参考答案(仅供参考)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | C | D | D | D | 如图,正方体AC1中,M是棱D1D的中点,O是正方形ABCD的中心,则异面直线OA1与AM所成的角是 A. | A | A | B | A |
6.  如图,正方体AC1中,M是棱D1D的中点,O是正方形ABCD的中心,则异面直线OA1与AM所成的角是
如图,正方体AC1中,M是棱D1D的中点,O是正方形ABCD的中心,则异面直线OA1与AM所成的角是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. 连B![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,故选A.
,故选A.
二.简答题答案:
11. ![]()
12. ![]()
13. ![]() ;
;
14. ![]()
![]()
15. 5![]()
三.解答题答案:
16.
|
![]() 中有
中有![]() ,
,
![]() 面ABCD.……………………4分
面ABCD.……………………4分
(2)取SD中点F,SC的中点G,
连AF、FG、EG,
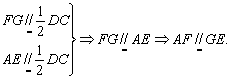
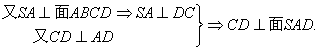 ……………………………6分
……………………………6分
|
|
∴二面角E—SC—D的平面角为90°.………………………………………………9分
(3)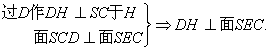
∴DH为点D到面SEC的距离 ∴DH·SC=SD·DC
![]() .
.
17. ⑴解法(一)(1)以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系0-xyz,则D(0,0,0),A(2,0,0),C(0,2,0),B(2,2,0),
A1(2,0,4),D1(0,0,4),C1(0,2,4),B1(2,2,4),
设E(0,2,t),则∵![]()
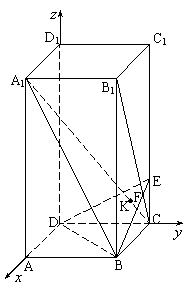
![]()
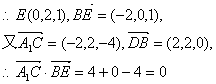
且![]()
![]()
![]()
(2)设A
设A
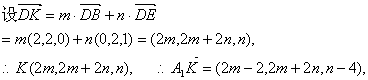
![]() …①
…①
同理有![]() …②
…②
由①,②联立解得![]()
![]()
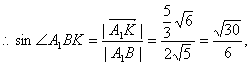 即所求角的正弦值是
即所求角的正弦值是![]()
解法(二)(1)证明:连AC交BD于点O,由正四棱柱性质可知AA1⊥底面ABCD,AC⊥BD,∴A
又∵A1B⊥侧面BC1且B
∵BD∩BE=B, ∴A
(2)解:设A
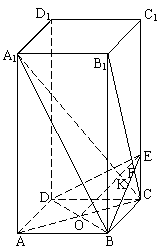 则∠A1BK为A1B与平面BDE所成的角,
则∠A1BK为A1B与平面BDE所成的角,
∵在侧面BC1中BE⊥B
![]()
连结OE,则OE为平面ACC
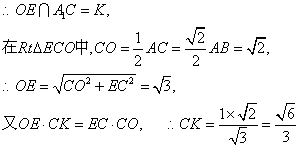
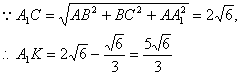
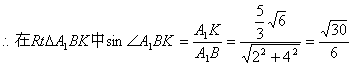
即为A1B与平面BDE所成的角的正弦值.
18. (1)证明:易证AD⊥面BB
![]()
19. 证明:(Ⅰ)作AD的中点O,则VO⊥底面ABCD.…………………………1分
建立如图空间直角坐标系,并设正方形边长为1,…………………………2分
则A(![]() ,0,0),B(
,0,0),B(![]() ,1,0),C(-
,1,0),C(-![]() ,1,0),D(-
,1,0),D(-![]() ,0,0),V(0,0,
,0,0),V(0,0,![]() ),
),
∴![]() ………………………………3分
………………………………3分
由![]() ……………………………………4分
……………………………………4分
![]() ……………………………………5分
……………………………………5分
又AB∩AV=A ∴AB⊥平面VAD…………………………………………6分
(Ⅱ)由(Ⅰ)得![]() 是面VAD的法向量………………………………7分
是面VAD的法向量………………………………7分
设![]() 是面VDB的法向量,则
是面VDB的法向量,则
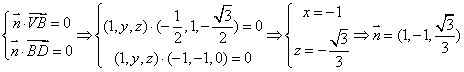 ……9分
……9分
∴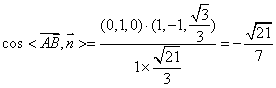 ,……………………………………11分
,……………………………………11分
又由题意知,面VAD与面VDB所成的二面角,所以其大小为![]() …………12分
…………12分
20. ∵P-ABD,Q-CBD是相同的正三棱锥,∴△这BD与△QBD是全等的等腰三角形,
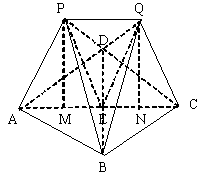 取BD中点E,连结PE,QE,则BD⊥PE,BD⊥QE
取BD中点E,连结PE,QE,则BD⊥PE,BD⊥QE
∴BD⊥平面PQE ,从而PQ⊥BD。
⑵证明:由⑴知∠PEQ是二面角P-BD-Q的平面角;
作PM⊥,垂足为M,作QN⊥,垂足为N,则PM//QN,M,N分别为正![]() 与正
与正![]() 的中心,从而A,M,E,N,C在一条直线上。
的中心,从而A,M,E,N,C在一条直线上。
PM与QN确定平面PACD且PMNQ为矩形
经计算![]() ,
,![]()
![]() ,
,
![]() 二面角
二面角![]() 为
为![]() 。
。
⑶解:由⑴知:![]() 平面PEQ,设点P到平面QBD的距离为h
平面PEQ,设点P到平面QBD的距离为h
则![]()
又![]()
![]() 。即点P到平面QBD的距离为
。即点P到平面QBD的距离为![]() 。
。
21. 方法1:如图AB1=AB+BB1,MN=0.5BC+CN
AB1·MN=(AB+BB1) ·(0.5BC+CN)=AB·(0.5BC)+AB·CN+BB1· (0.5BC)+BB1·CN
=0.5×1×1(﹣0.5)+0+0+2CN=0 ∴CN=0.125
![]()
由A1S1·MN=0 得 Z=0.125
AC所在直线的x轴 AA1所在直线为y轴 A为原点
方法3:AB1在面BCC1B1的射影为B
![]()
由勾股定理x=0.125.