高二数学秋学期期末考试试卷

高二数学秋学期期末考试试卷

高二数学

一、选择题（本大题共有12小题, 每小题5分, 共60分. 在每小题所给出的四个选项中，只有一项是符合题意的，请把正确选项前的字母代号填在题后的括号内）

1．物体的运动方程是S=10t－t² (S的单位：m； t的单位：s), 则物体在t=2s的速度是 　　( 　　)　　　　　　　　　　　　　　　　　　　　　　　　　 

　A．2 m/s　　 　B．4 m/s　　　　 　C．6 m/s　　　　D．8 m/s

2．算法　

　　　　　　　　　　　　　　　　　  此算法的功能是　　　　　　　　　　　 　　 (　 　 )

A．a，b，c中最大值　　　　　 B．a，b，c中最小值

C．将a，b，c由小到大排序　　D．将a，b，c由大到小排序

3．从一群游戏的孩子中抽出k人，每人扎一条红带，然后让他们返回继续游戏，一会后，

再从中任取m人，发现其中有n人扎有红带，估计这群孩子的人数为　　　　 　　（ 　　 ）　

　　A．k m　　　　　 B．k n　　　　　　  C．　　　　　  D．

4．甲、乙、丙、丁四名射击选手在选拔赛

	甲	乙	丙	丁
	8	9	9	8
	5．7	6．2	5．7	6．4

中所得的平均环数及其方差S²如下表

所示，则选送参加决赛的最佳人选

是 　　　　　　　　　　　（　　 ）

　 A．甲　　　　  B． 乙　　

 C．丙　　　　  D． 丁

5．若命题p: xA∪B, 则非p是　　　　　　　　　　　　　　　　　　　　　　 　　　(　　　)

　 A．xA且xB　 　B．xA或xB 　　C．xA∩B  　　D．xA∩B

6．在下列命题中，

(1).　 (2),使得x²+x+1<0.　(3)若tan= tan,则=.

(4)若ac=b²则a、b、c成等比数列。 其中真命题有　　　　　　　　　　　　 　　　（　　　）

A．0个　　　 　　B．1个　　　　　  C．2个　　　　  D．3个

7．若不等式x－1 <a成立的充分条件是0<x<4,则实数a的取值范围是　　　　　　 　　　(　　　)

　 A．a1　　　 B．a3　　　　  C．a1　　　　 D．a3

8． (文科做) 甲、乙两人下棋，两人下成和棋的概率是，乙获胜的概率是则是　　　(　　　）

A．乙胜的概率　 B．乙不输的概率　　C．甲胜的概率　　D．甲不输的概率

8．(理科做)若向量、的坐标满足，，则·等于　(　　 )

　A． 　　　 　 　B．　　　　 　C．　　 　　　　　 　D．

9．(文科做) 设一组数据的方差s²,将这组数据的每个数据乘以10,所得到一组新数据的方差是 (　　)　

　 A．0.1s²　　　　 B．100s²　　　　  C．10s²　　　　　  D．s²　

9．(理科做)下列积分正确的一个是　　　　　　　　　　　　　　　　　　　　　 　　　( 　 　)

 A．sinx dx=2　　　　　　　　　 B．=12　

 C．e ^x (1+ e ^x ) dx =　　　　　 D．dx =－e  

10．已知双曲线 － =1(a>)的两条渐近线的夹角为,则双曲线的离心率为　 　 (　 　 )

A．2　　　　　  B．　　　　　 C．　　　　 D．

11．在平面直角坐标系中，点(x,y) 中的x、y∈{0,1,2,3,4,5,6}且x≠y，则点(x,y)落在半圆

（x－3）²+y²=9(y≥0)内(不包括边界) 的概率是　　　　　　　　　　　　　　 　　（ 　　 ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

 A．　　　　  B．　　　　　　　 C．　　　　　　  D．

12．函数y=xcosx－sinx在下面哪个区间上是增函数　　　　　　　　　　　　　　　  (　　 )

　　A．(, )　　B．(π, 2π)　　 C．( ,)　  D．( 2π, 3π)

二、填空题（本大题共有6小题，每题5分，共30分. 把结果直接填在题中的横线上）

13．若施肥量x与水稻产量y的线性回归方程为=5x+250，当施肥量为80kg时，预计的水

稻产量为 　　　　　  .

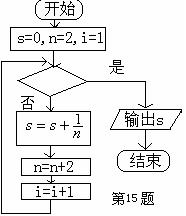
14.右图给出的是计算的值的一个程序

　 框图，其中判断框内应填入的条件是　　　　　　 .

15有两个人在一座层大楼的底层进入电梯，设他们中的每

　 一个人自第二层开始在每一层离开是等可能的，则这两个

　 人在不同层离开的概率是　　　　．

16．直线y＝x－3与抛物线y²=4x 交于A、B两点，过A、B

　 两点向抛物线的准线作垂线，垂足分别为P、Q，则梯形

　 APQB的面积为　　　　　  ．

17．点P是椭圆上一点, F₁、F₂是其焦点, 若

　 ∠F₁P F₂=90°, △F₁P F₂面积为　　　　 ．

18. (文科做) 函数f(x)= x－e^x在点P的切线平行于x轴,则点P的坐标为　　　　  ．

18. (理科做) 由曲线y=、直线x=1、x=6和x轴围成的封闭图形的面积为　　　　 ．

三、解答题（本大题共有6小题，满分50分. 解答需写出文字说明、推理过程或演算步骤）

19.一个社会调查机构就某地居民的月收入调查了20000人，并根据所得数据画了样本的频率分布直方图（如下图）．

根椐上述信息回答下列问题：

（1）月收入在[3000, 3500 )的居民有多少人?

(2) 试估计该地居民的平均月收入（元）；

(3) 为了分析居民的收入与年龄、学历、职

业等方面的关系，要从这20000人中再用分层抽样方法抽出300人作进一步调查，则在[2500, 3000 )（元）月收入段应抽出多少人．

20.今有一批球票，按票价分别为10元票5张，20元票3张，50票2张，从这批票中抽出2

张. 问：

 （1）抽得2张均为20元的票价的概率

（2）抽得2张不同票价的概率.

（3）抽得票价之和等于70元的概率.

21.(文科做)已知命题p: f (x)= , 且,命题q: 集合,

B={x x＞0}, 且，求实数a的取值范围，使p、q中有且只有一个为真命题。

21. (理科做)如图，在正方体中，是棱的中点，为平面

内一点，。

（1）证明平面；

（2）求与平面所成的角；

（3）若正方体的棱长为，求三棱锥的体积。

22．点M是曲线C上任意一点,它到F(4,0)的距离比它到直线x+2=0的距离大2, 且P(2m, m)(m>0),

　　，均在曲线C上．

（1）写出该曲线C的方程及 m的值；

（2）当PA与PB的斜率存在且倾斜角互补时，求的值及直线AB的斜率．

23．已知双曲线(a＞0,b＞0)的左顶点为A，右焦点为F ，过点F作垂直于x轴的直线与双曲线交于 B、C 两点，且

　（1）求双曲线的方程；

（2）过F的直线l交双曲线左支D点,右支E点, P为DE的中点,若以AF为直径的圆恰好经过P

　　点,求直线l的方程．

　

24．已知函数=，在x=－1处取得极值2．

（1）求函数的解析式；

（2）满足什么条件时，区间为函数的单调减区间？

（3）若为=图象上的任意一点，直线与=的图象切于点，

　　求直线的斜率的取值范围．

答案

一．选择题

1．C　2.A　3.D　4.C　5.A　6.B　7D　8.B　9.B　10.D　11.B　12.C

二．填空题

13. 650 　　14.n≥20　　 15. 　 16. 48　　17. 9　 18. (0,-1) 18.

三．解答题.

19解：（1）由频率分布直方图可知: 距(4000－1000)÷6=500,

在[3000,3500)内的频率为0.0003×500=0.15

∴ 月收入在[3000, 3500 )的居民有20000×0.15=3000（人）

　　（2）各组的频率分别为：0.1、0.2、0.25、0.25、0.15、0.05.　

　　　 1250×0.1+1750×0.2 +2250×0.25+2750×0.25+3250×0.15+3750×0.05=2400（元）

　　　估计该地居民的平均月收入为2400（元）　　　　　　

（3）在[2500, 3000 )组中的频率为0.25

　　∴在[2500, 3000 )（元）月收入段应抽出300×0.25=75（人）　　　　

20. 解: (1)分别记10元票为1、2、3、4、5号，20元票为6、7、8号，50票为9、10号。

　　　从中抽出2张，有如下基本事件（抽出1、2号用（1，2）表示）：

（1，2），（1，3），（1，4），……（1，10），

（2，3），（2，4），……（2，10），

（3，4），……（3，10），

……

（10，10），

　　　 共有9+8+7+…+1=45个基本事件.

设抽得2张均为20元的票价的事件为A, 即: (6,7), (6,8), (7,8) , 故P(A)==

∴抽得2张均为20元的票价的概率为

 (2) 设抽得2张不同票价的事件为B, 则对立事件 为抽得2张相同票价的事件

即: 2张10元票（1,2），（1,3），（1,4），(1,5),（2,3），（2,4）,(2, 5), (3, 4).(3, 5),(4, 5),

2张20元票 (6,7), (6,8),　(7,8)

2张50元票 (9,10)

　　共有10+3+1=14个结果,　∴P(B)=1－P()=1－=

即抽得2张不同票价的概率为

 (3) 设抽得票价之和等于70元的事件为C, 即1张20元, 1张50元,因此有(6,9),(610),

　 (7,9),(7,10),(8,9),(8,10) ,共有6个结果, P(C)==.

∴抽得票价之和等于70元的事件概率为.

21.(文科)

解：命题p: f（x）＜2,  

命题q: 设判别式为

当时，，此时，

当时，由得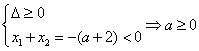

∴ a>-4

（1）若p真q假--------------------2

（2）若p假q真---------------------2

∴ 实数a的取值范围为　

 21. (理科)

解(1)设正方体的棱长为，

则，，

∵，　

∴，又，

∴平面。

　 （2），设与所成的角为，

，

∴。

　　　　由（1）知平面，∴为与平面所成的角。。

　 （3）

22解：（1）由题意: M是曲线C上任意一点,它到F(4,0)的距离比它到直线x+2=0的距离大

2, 因此, 它到F(4,0)的距离等于它到直线x+4=0的距离,根据圆锥曲线的定义可

知曲线C为抛物线, 且以F(4,0)为其焦点,

设y²=2px,  =4,　2p=16　∴曲线C的方程为　　

又P(2m, m)在曲线C 上,　 ∴ m=4　　　　　　　　　　

　　 （2）PA，ＰＢ倾斜角互补且斜率存在

……8分

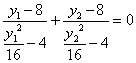由得，即

　 　

　

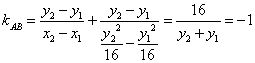
23. 解 (1) ∵AB⊥AC，BC⊥x轴, BC=6, ∴AF=a+c=6,

　　直线BC: x=c, 代入,得: y²=, B(c, ), C(c, －).

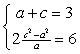∴ ∴a=1,c=2, 从而b²=3

 所求双曲线的方程为x²－=1.

 (2) 设直线l的方程为y=k(x－2), 代入3x²－y²=3,得: (3－k²) x² +4k²x－4k²－3=0

　　　，由题意x₁ x₂=＜0, ∴ －＜k＜

　　　x_{1 +} x₂=, y₁+y₂=k(x_{1 +} x₂)－4 k=

∵P为DE的中点, ∴P(,),　A(－1,0) , F(2,0)

　　又∵以AF为直径的圆恰好经过P点, ∴=0

　 (+ 1, )(－2, )=0,

(+ 1)( －2)+ ()²=0, 化简得54k²=18,　k=±

此时直线l的方程y=±(x－2).

24.解：（1）已知函数=，

又函数在x=－1处取得极值2，∴，即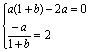

　　　　　　　　　　　　　　　　 

（2）　　　 由

x			（-1，1）	1
	+	0	－	0	+
		极大值 2		极小值－2

所以　 的单调减区间为，　　　　 

∵为函数的单调减区间，∴有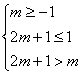

解得　　　　　　　　　　　

即时，为函数的单调减区间。

（3） ,

直线的斜率为　

令，则直线的斜率，　　　　

∴.