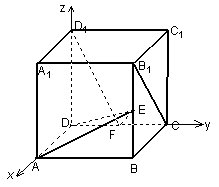
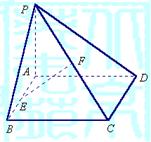
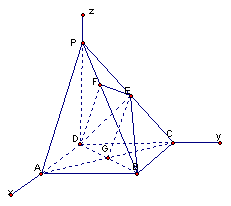
第九章 单元测试(三)-----------空间向量及坐标运算
一、选择题(本大题共6小题,每小题6分,共36分.把答案填在答卷上)
1.O、A、B、C为空间四个点,又![]() 、
、![]() 、
、![]() 为空间的一个基底,则( )
为空间的一个基底,则( )
A.O、A、B、C四点共线 B.O、A、B、C四点共面
C.O、A、B、C四点中任三点不共线 D.O、A、B、C四点不共面
2.a、b为非零向量,命题甲:“向量a与向量b平行”.命题乙:“a+b=a+b,那么命题甲是命题乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.AD为△ABC的角平分线,且![]() =c,
=c,![]() =b,设
=b,设![]() =λ
=λ![]() ,则λ的值为( )
,则λ的值为( )
A.![]() B.
B.![]() C.
C.![]() D.-
D.-![]()
4.在下列命题中:①若![]() 、
、![]() 共线,则
共线,则![]() 、
、![]() 所在的直线平行;②若
所在的直线平行;②若![]() 、
、![]() 所在的直线是异
所在的直线是异
面直线,则![]() 、
、![]() 一定不共面;③若
一定不共面;③若![]() 、
、![]() 、
、![]() 三向量两两共面,则
三向量两两共面,则![]() 、
、![]() 、
、![]() 三向量一定也共面;④已知三向量
三向量一定也共面;④已知三向量![]() 、
、![]() 、
、![]() ,则空间任意一个向量
,则空间任意一个向量![]() 总可以唯一表示为
总可以唯一表示为
![]() .其中正确命题的个数为
( )
.其中正确命题的个数为
( )
A.0 B.
5.已知三角形的顶点A(1,-1,1),B(2,1,-1),C(-1,-1,-2),这个三角形的面积是( )
A.![]() B.
B.![]() C.2
C.2![]() D.
D.![]()
6.已知点![]() ,且该点在三个坐标平面
,且该点在三个坐标平面![]() 平面,
平面,![]() 平面,
平面,![]() 平
平
面上的射影的坐标依次为![]() ,
,![]() 和
和![]() ,则( )
,则( )
A.![]() B.
B. ![]()
![]() C.
C. ![]() D.
D.![]() 以上结论都不对
以上结论都不对
二、填空题(本大题共4小题,每小题6分,共24分.把答案填在答卷上)
7.已知a=(2,-3,5),b=(-3,1,-4),则a·b的值为___▲________.
8已知![]() 为单位正交基,且
为单位正交基,且![]() ,则向量
,则向量![]() 与
与
向量![]() 的坐标分别是_______▲_______;__________▲_______.
的坐标分别是_______▲_______;__________▲_______.
9.设![]() 的夹角为
的夹角为![]() ;则
;则![]() 等于________▲______.
等于________▲______.
10.已知ABCD—A′B′C′D′是平行六面体,E、F分别是棱![]() 、
、![]() 的中点,则化简
的中点,则化简![]()
![]() +
+![]() +
+![]()
![]() =_____▲______.
=_____▲______.
班级 姓名 学号
| 一 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
二填空题:
7. ;8。 ; ;9。 ;10。 ;
三、解答题(本大题4小题,每题10分,满分40分
11.设向量![]() 并确定
并确定![]() 的关系,使
的关系,使![]() 轴垂直.
轴垂直.
|
(1)求EF的长;
(2)求证:![]() 平面ADE。
平面ADE。

13.已知两个半平面的交线上有两个点A、B,AC、BD分别在两个半平面内且垂直于线段AB,AC与BD所成的角为![]() ,又AC=AB=BD=
,又AC=AB=BD=![]() ,求CD的长。
,求CD的长。
14.如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、
|
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°,求EF与AP所成的角的大小.
参考答案:
D、B、B、A、A、A
-29;(1,-2,1),(-5,7,7);2;![]()
11.解:![]() (9,15,-12)-(4,2,16)=(5,13,-28)
(9,15,-12)-(4,2,16)=(5,13,-28)
![]() (3,5,-4)
(3,5,-4)![]() (2,1,8)=6+5-32=-21
(2,1,8)=6+5-32=-21
由![]()
![]()
![]()
即当![]() 满足
满足![]() =0即使
=0即使![]() 与z轴垂直.
与z轴垂直.
12.(12分) 解:建立如图所示的直角坐标系,(1)不妨设正方体的棱长为1,
|
E(1,1,![]() ),F(0,
),F(0,![]() ,0),
,0),
则![]() =(0,
=(0,![]() ,-1),
,-1),![]() =(1,0,0),
=(1,0,0),
![]() =(0,1,
=(0,1,![]() ),
则
),
则![]() =0,
=0,
![]() =0,
=0, ![]() ,
,![]() .
.
![]() 平面ADE.
平面ADE.
(2)![]() (1,1,1),C(0,1,0),故
(1,1,1),C(0,1,0),故![]() =(1,0,1),
=(1,0,1),![]() =(-1,-
=(-1,-![]() ,-
,-![]() ),
),
![]() =-1+0-
=-1+0-![]() =-
=-![]() ,
, ![]() ,
,![]() ,
,
|
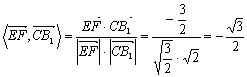 .
. 13.![]() 或2
或2
14.(12分) 证:如图,建立空间直角坐标系A-xyz,设AB=
BC=2b,PA=
D(0, 2b,
0),P(0, 0,
∴ E (a, 0, 0),F (a, b, c)
(1)∵ =(0, b, c),=(0, 0,
∴ =(+) ∴ 与、共面
又∵ E Ï 平面PAD ∴ EF∥平面PAD.
(2) ∵ =(
∴ CD⊥EF.
(3) 若ÐPDA=45°,则有2b=
=(0, 0, 2b) ∴ cos á,ñ== ∴ á,ñ= 45°