高二数学单元试题

（考试时间：120分钟　 满分：150分）

一．选择题（本大题共12小题，每小题5分，共60分）

1．已知向量a＝（1，1，0），b＝（－1，0，2），且a＋b与2 a－b互相垂直，则的值是（　　 ）

A．　1　　　 B．　 　　　　C．　 　　　　D．

2．已知（　　  ）

A．－15　　　　　　　　　 B．－5　　　　　　　　　　 C．－3　　　　　　　　　　 D．－1

3．已知A、B、C三点不共线，对平面ABC外的任一点O，下列条件中能确定点M与点A、B、C一定共面的是　　　　　　　　　 （　　　 ）

　　　 A．　　　　　　　　　　 B．

　　　 C．　　 　　　 D．

4．已知向量a＝（0，2，1），b＝（－1，1，－2），则a与b的夹角为　（　　  ）

A．　0°　　　　  B．　 45°　　  C．　90°　　　　D．180°

5．已知△ABC的三个顶点为A（3，3，2），B（4，－3，7），C（0，5，1），则BC边上的中线长为　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　 （　　 ）

A．2　　　　　　　　　B．3 　　　　　　　　 C．4　　　　　　　　　　 D．5

6．在下列命题中：①若a、b共线，则a、b所在的直线平行；②若a、b所在的直线是异面直线，则a、b一定不共面；③若a、b、c三向量两两共面，则a、b、c三向量一定也共面；④已知三向量a、b、c，则空间任意一个向量p总可以唯一表示为p＝xa＋yb＋zc．其中正确命题的个数为（　　 ）

A． 0　　　　　　 B．1　　　　　　 C． 2　　　　　　 D．3

7．已知空间四边形ABCD，M、G分别是BC、CD的中点，连结AM、AG、MG，则+等于（　　  ）　　　　　　　　　　

A．　　　　　  B． 　　　　　 C． 　　　　　 D．　

8．直三棱柱ABC—A₁B₁C₁中，若，，， 则　　 （　　 ）

A． 　　　B．　　  C． 　　　　D．

9．在平行六面体ABCD－A₁B₁C₁D₁中，向量、、是　 （　　　）

　　　 A．有相同起点的向量　　　　　　　　　　　　　B．等长向量　　

　　　 C．共面向量　　 　　　　　　　　　　　　　　　　　 D．不共面向量

10．已知点A（4，1，3），B（2，－5，1），C为线段AB上一点，且,则点的坐标是　　　　　　  (　　　 )

　 A．　　　 B．　　　 C． 　　　D．

11．设A、B、C、D是空间不共面的四点，且满足，则△BCD是 （　　 ）

　 A．钝角三角形　　　 B．直角三角形　　 C．锐角三角形　　 D．不确定

12．（文科）在棱长为1的正方体ABCD—A₁B₁C₁D₁中，M和N分别为A₁B₁和BB₁的中点，那么直线AM与CN所成角的余弦值是（　　 ）

　　　 A．　　　　　 B．　　　　　　  C．　　　　  　　D．

（理科）已知正方形ABCD的边长为4，E、F分别是AB、AD的中点，GC⊥平面ABCD，且GC＝2，则点B到平面EFG的距离为（　　 ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

A．　 　　　B．　　　　　 C． 　　　 D． 1

二．填空题（本大题4小题，每小题4分，共16分）

13．已知向量a=(+1,0,2)，b=(6,2-1,2),若a∥b,则与的值分别是　　　　　　　　  ．

14．已知a,b,c是空间两两垂直且长度相等的基底，m=a+b,n=b-c,则m，n的夹角为 　　　　　　．

15．已知向量a和c不共线，向量b≠0，且，d＝a＋c，则＝　　　　　  ．

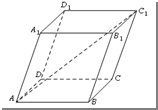
16．（如图）一个结晶体的形状为平行六面体，其中，以顶点为端点的三条棱长都等于1，且它们彼此的夹角都是，那么以这个顶点为端点的晶体的对角线的长为　　　　　　  。

高二数学单元测试答题卷

一．选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	A	D	C	B	A	A	D	C	C	C	B

二．填空题

13．________、_________、．14．____________________．60°

15．_________________．90°16．_____________________．

三．解答题（本大题6小题，共74分）

17．（本小题满分12分）

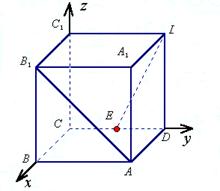如图，在棱长为2的正方体ABCD－A₁B₁C₁D₁中，E是DC的中点，取如图所示的空间直角坐标系．

　 （1）写出A、B₁、E、D₁的坐标；

　 （2）求AB₁与D₁E所成的角的余弦值．　

解：(1) A(2, 2, 0)，B₁(2, 0, 2)，E(0, 1, 0)，D₁(0, 2, 2)

　　　　  (2)∵ ＝(0, -2, 2)，＝(0, 1, 2)　∴ ＝2，＝，·＝0－2＋4＝2,

∴ cos á，ñ ＝ ＝ ＝ ．∴ AB₁与ED₁所成的角的余弦值为．

18．（本小题满分12分）

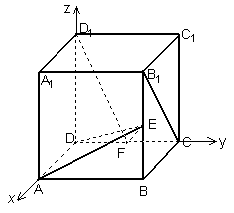在正方体中，如图Ｅ、Ｆ分别是，ＣＤ的中点，

（1）求证：平面ADE；

（2）cos．　　　

解：建立如图所示的直角坐标系，（1）不妨设正方体的棱长为1，

则D（0，0，0），A（1，0，0），（0，0，1），

　　　　 E（1，1，），F（0，，0），

　　　　 则＝（0，，－1），＝（1，0，0），　　

　　　　 ＝（0，1，），  则＝0，

　　　　 ＝0， ，.　　

　　　　 平面ADE.

（２）（1，1，1），C（0，1，0），故＝（1，0，1），＝（－1，－，－），

　　　　 ＝－1＋0－＝－，　　 ，，　　

则cos.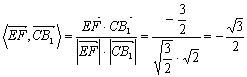

19．（本小题满分12分）

如图，在四棱锥中，底面ABCD是正方形，侧棱底面ABCD，

　　　，E是PC的中点，作交PB于点F.

　 （1）证明 平面；

　 （2）证明平面EFD．

解：

解：如图所示建立空间直角坐标系，D为坐标原点.设

(1)证明：连结AC，AC交BD于G.连结EG.

　　　　 依题意得

　　　　 底面ABCD是正方形， 是此正方形的中心，

　　　　 故点G的坐标为且

　　　　 . 这表明.

　　　　 而平面EDB且平面EDB，平面EDB。

(2)证明：依题意得。又故　

　　　　 , 由已知，且所以平面EFD.

20．（本小题满分12分）

如图，四边形ABCD是直角梯形，∠ABC＝∠BAD＝90°，

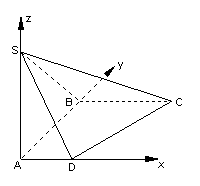SA⊥平面ABCD， SA＝AB＝BC＝1，AD＝．

（1）求SC与平面ASD所成的角余弦；

（2）求平面SAB和平面SCD所成角的余弦．

解：

（1）　（2）

21．（本小题满分12分）

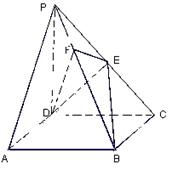
如图，在底面是菱形的四棱锥P—ABCＤ中，∠ABC=60⁰，PA=AC=a，PB=PD=,点E在PD上，且PE:ED=2:1.

（1）证明PA⊥平面ABCD；

（2）求以AC为棱，EAC与DAC为面的二面角的大小

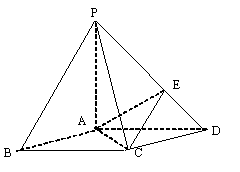（1）证明　因为底面ABCD是菱形，∠ABC=60°，

所以AB=AD=AC=a，　在△PAB中，

由PA²+AB²=2a²=PB²　 知PA⊥AB.

同理，PA⊥AD，所以PA⊥平面ABCD.

（2）解　作EG//PA交AD于G，

由PA⊥平面ABCD.

知EG⊥平面ABCD.作GH⊥AC于H，连结EH，

则EH⊥AC，∠EHG即为二面角的平面角.

又PE : ED=2 : 1，所以

从而　　

22．（本小题满分14分）

P是平面ABCD外的点，四边形ABCD是平行四边形，

.

（1）求证：PA平面ABCD.

（2）对于向量，定义一种运算：

，

试计算的绝对值;说明其与几何体P-ABCD的体积关系，并由此猜想向量这种运算的绝对值的几何意义（几何体P-ABCD叫四棱锥，锥体体积公式：V=）.

解：

（1）

　　　　

　　　　　

　　　　

（2）

V＝

猜测：在几何上可表示以AB,AD,AP为棱的平等六面体的体积（或以AB,AD,AP为棱的四棱柱的体积）