第九章 单元测试（四）------空间的角
一、选择题（6×6＝36）
1、已知
则
与
的夹角等于 （ ）
A．90° B．30° C．60° D．150°
2.一条直线和平面所成角为θ，那么θ的取值范围是（ ）
（A）（0º,90º） （B）[0º,90º] （C）[0º,180º] （D）（0º,180º）
3. 直线l与平面α成角为
，直线
平面α，且与直线l异面，则直线l与直线a所成角的取值范围是（ ）
A. 
B.
C. 
D. 
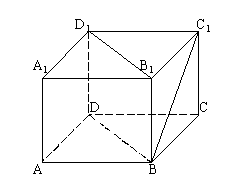
4. 如下图所示，已知长方体
中，AB＝BC＝4，
，则直线
和平面
所成角的正弦值等于（ ）
A. 
B.
C.
D.
5．
在正三角形ABC中，AD⊥BC于D，沿AD折成二面角B—AD—C后，
，这时二面角B—AD—C的大小是（ ）
A. 60° B. 90° C. 45° D. 120°
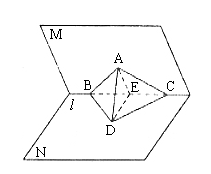
6. 如下图所示，在二面角M—l—N的面M内，有Rt△ABC，斜边BC在棱上，若A在平面N内的射影为D，且∠ACD＝
，∠ABD＝
，二面角为θ，那么
，θ间应满足（ ）
A. 
B. 
C. 
D. 
二、填空题（4×6＝24）
7. 已知二面角
为
，异面直线a、b分别垂直于
与
，则a与b所成角为▲
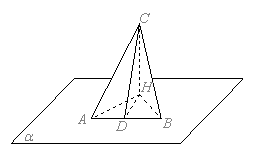
8、在三棱锥P—ABC中，PA=PB=PC=AB=AC，且
，则PA与ABC所成角为▲
9、在正方体
中，面对角线
与对角面
所成的角为 ▲
10．在600的二面角的棱上有两点A、B，AC、BD分别是在这个二面角的两个面内垂直于AB的线段，已知：AB=6，AC=3，BD=4，则CD= ▲ 。
班级 姓名 学号
| 一 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
二填空题：
7． ；8。 ；9。 ；10。 ；
三、解答题（4×10＝40）
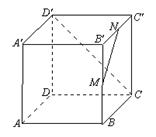
11． 如图，M、N分别是棱长为1的正方体
的棱
、
的中点．求异面直线MN与
所成的角．
12．直角
的斜边
在平面内，
与所成角分别为
，
是斜边上的高线，求与平面所成角的正弦值
13．如果二面角
的平面角是锐角，点
到
的距离分别为
，求二面角的大小
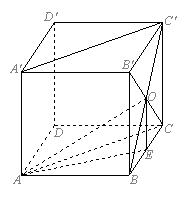14．如图，正方体的棱长为1，
，求：（1）
与平面
所成角的正切值；（2）平面
与平面
所成角
【试题答案】
1. D 2、B 3、D 4. C 5 A
6. B
7、 8、
9、
10、7
4．直角的斜边在平面内，与所成角分别为，是斜边上的高线，求与平面所成角的正弦值
解：过点
作
于点
，连接
，
则
，
，
为所求与所成角，记为
，
令
，则
，
则在
中，有
在
中，
∴与平面所成角的正弦值
.
5．如果二面角的平面角是锐角，点到的距离分别为
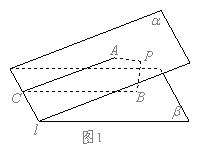
，求二面角的大小
分析：点可能在二面角内部，也可能在外部，应区别处理
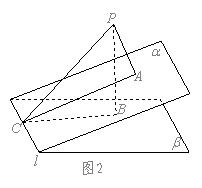
解：如图1是点在二面角的内部时，图2是点在二面角外部时，
∵
∴
∵
∴面
同理，面
而面
面
∴面
与面
应重合
即
在同一平面内，
则
是二面角的平面角
在
中，
∴
在
中，
∴
故
（图1）或
（图2）
即二面角的大小为
或
说明：作一个垂直于棱的平面，此平面与两个半平面的交线所成的角就是二面角的平面角
6．如图，正方体的棱长为1，，求：
（1）与
所成角；
（2）与平面所成角的正切值；
（3）平面与平面所成角
解：（1）∵
∴与所成角就是
∵
平面
∴
（三垂线定理）
在
中， 
∴
（2）作
，平面
平面
∴
平面，
为
与平面所成角
在
中，
∴
（3）∵
∴
平面
又∵
平面 ∴平面
平面
即平面与平面所成角为